题目内容
12.对于正数x,规定f(x)=$\frac{1}{1+x}$,例如:f(4)=$\frac{1}{1+4}$=$\frac{1}{5}$,f($\frac{1}{4}$)=$\frac{1}{1+\frac{1}{4}}$=$\frac{4}{5}$,则f(2017)+f(2016)+…+f(2)+f(1)+f($\frac{1}{2}$)+…+f($\frac{1}{2016}$)+f($\frac{1}{2017}$)=$\frac{4033}{2}$.分析 根据f(x)=$\frac{1}{1+x}$可得出f($\frac{1}{x}$)=$\frac{x}{1+x}$,将其相加即可得出f(x)+f($\frac{1}{x}$)=1,由此即可得出原式=2016×1+f(1),代入x=1即可得出结论.
解答 解:∵f(x)=$\frac{1}{1+x}$,f($\frac{1}{x}$)=$\frac{1}{1+\frac{1}{x}}$=$\frac{x}{1+x}$,
∴f(x)+f($\frac{1}{x}$)=$\frac{1}{1+x}$+$\frac{x}{1+x}$=1.
∴f(2017)+f(2016)+…+f(2)+f(1)+f($\frac{1}{2}$)+…+f($\frac{1}{2016}$)+f($\frac{1}{2017}$)=1+1+…+1+f(1)=2016×1+f(1)=2016+$\frac{1}{2}$=$\frac{4033}{2}$.
故答案为:$\frac{4033}{2}$.
点评 本题考查了函数值以及规律性中数的变化类,根据函数关系式找出f(x)+f($\frac{1}{x}$)=1是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3.关于x的不等式x-b≥0恰有两个负整数解,则b的取值范围是( )
| A. | -3<b<-2 | B. | -3<b≤-2 | C. | -3≤b≤-2 | D. | -3≤b<-2 |
7.若x>y,则下列式子错误的是( )
| A. | x-2>y-2 | B. | x+1>y+1 | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | -5x>-5y |
1.一元二次方程x2-2x-3=0的根的情况是( )
| A. | 没有实数根 | B. | 有个相等实根 | C. | 有两个不等实根 | D. | 无法确定 |
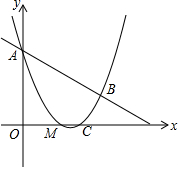 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A、B两点,交x输的右交点为C,己知A(0,3),C(3,0),P为线段AB上一动点(不含端点).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A、B两点,交x输的右交点为C,己知A(0,3),C(3,0),P为线段AB上一动点(不含端点). 如图是小明设计的一个飞镖靶子,他把四个同心圆六等份,涂上颜色,那么,投中白色部分的可能性大小是$\frac{1}{2}$.
如图是小明设计的一个飞镖靶子,他把四个同心圆六等份,涂上颜色,那么,投中白色部分的可能性大小是$\frac{1}{2}$.