题目内容
7.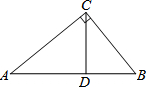 如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.
如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.
分析 设BD=x,则AD=4x,然后根据已知条件可以证明△ADC∽△CDB,根据其对应边成比例求出CD=2x,最后根据tan∠BCD的定义即可求出其值.
解答 解:
∵BD:AD=1:4,设BD=x,则AD=4x.
在△ACD和△CBD中,∠A+∠B=90°,∠B+∠BCD=90°,
∴∠CAD=∠BCD.
又∵∠ADC=∠CDB=90°,
∴△ADC∽△CDB.
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$,即CD2=AD•BD,
∴CD2=4x2,
∴CD=2x.
那么tan∠BCD=$\frac{BD}{CD}$=$\frac{x}{2x}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查三角函数的定义和相似三角形的判定和性质,利用相似三角形的性质求得BD和CD的关系是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
15.若点P(a,4-a)是第二象限的点,则a必须满足( )
| A. | a<0 | B. | a<4 | C. | 0<a<4 | D. | a>4 |
12.目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )
| A. | 438(1+x)2=389 | B. | 389(1+x)2=438 | C. | 389(1+2x)=438 | D. | 438(1+2x)=389 |
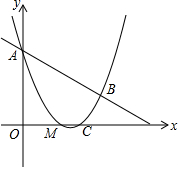 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A、B两点,交x输的右交点为C,己知A(0,3),C(3,0),P为线段AB上一动点(不含端点).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A、B两点,交x输的右交点为C,己知A(0,3),C(3,0),P为线段AB上一动点(不含端点).



 如图:直线a∥b,∠1=42°,则∠2=138°.
如图:直线a∥b,∠1=42°,则∠2=138°.