题目内容
20.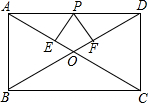 如图,在矩形ABCD中,
如图,在矩形ABCD中,(1)若AC=10,则AO=5,BO=5.
(2)若OD=5,AB=6,则BC=8,△BOC的周长为18.
分析 (1)根据矩形的对角线相等且互相平分解答即可;
(2)由OD的长可求出AC,再根据勾股定理即可求出BC的长;进而可求出△BOC的周长.
解答 解:
(1)∵四边形ABCD是矩形,
∴AC=BD=10,AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,
∴AO=5,BO=5.
故答案为:5,5;
(2)∵四边形ABCD是矩形,
∴AC=BD=2OD=10,∠ABC=90°,
∵AB=6,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=8,
∴△BOC的周长=5+5+8=18,
故答案为:8,18.
点评 本题考查了矩形的性质以及勾股定理的运用,熟记矩形的各种性质是解题的关键.

练习册系列答案
相关题目
8.已知方程x2+2x-1=0,则此方程( )
| A. | 无实数根 | B. | 两根之和为2 | C. | 两根之积为-1 | D. | 有一个根为$1+\sqrt{2}$ |
15.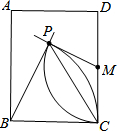 如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
 如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
9.下列命题中,假命题是( )
| A. | 矩形的对角线相等 | |
| B. | 菱形的面积等于两条对角线乘积的一半 | |
| C. | 对角线互相垂直的矩形是正方形 | |
| D. | 有两个角相等的梯形是等腰梯形 |
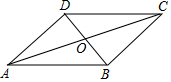 如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.