题目内容
5.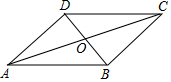 如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,AD=3$\sqrt{3}$,BD=6,AC=12,则?ABCD的面积是18$\sqrt{3}$.
分析 首先利用勾股定理的逆定理可证明△AOD是直角三角形,得出AD⊥BD,即可求出?ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,
∴AO=CO=$\frac{1}{2}$AC=6,BO=DO=$\frac{1}{2}$BD=3,
∵AD=3$\sqrt{3}$,
∴DO2+AD2=AO2=36,
∴△AOD是直角三角形,
∴AD⊥BD,
∴?ABCD的面积=AD•BD=3$\sqrt{3}$×6=18$\sqrt{3}$;
故答案为:18$\sqrt{3}$.
点评 本题考查了平行四边形的性质、勾股定理的逆定理以及三角形的面积公式的运用,解题的关键是证明△AOD是直角三角形.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
16.已知方程组$\left\{\begin{array}{l}{2x-3y=4}\\{ax+3y=9}\end{array}\right.$ 无解,则a的值是( )
| A. | 2 | B. | -2 | C. | 4.5 | D. | -4.5 |
13. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. |  | B. |  | C. |  | D. |  |
10.下列各式中,计算错误的是( )
| A. | [(a+b)2]5=(a+b)10 | B. | [(a+b)2]n=(a+b)n+2 | C. | [(a+b)x]5=(a+b)5x | D. | [(a+b)m]n=(a+b)mn |
17.下列图形中,不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 正八边形 | D. | 等边三角形 |
14.到三角形三个顶点的距离都相等的点是这个三角形的( )
| A. | 三条高的交点 | B. | 三条角平分线的交点 | ||
| C. | 三条边的垂直平分线的交点 | D. | 三条中线的交点 |
 如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是约为2.29海里(用科学计算器计算,使结果精确到0.01).
如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是约为2.29海里(用科学计算器计算,使结果精确到0.01).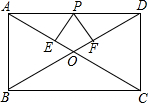 如图,在矩形ABCD中,
如图,在矩形ABCD中,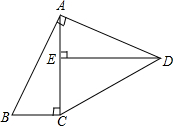 如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.