题目内容
8.已知方程x2+2x-1=0,则此方程( )| A. | 无实数根 | B. | 两根之和为2 | C. | 两根之积为-1 | D. | 有一个根为$1+\sqrt{2}$ |
分析 A、根据方程的系数结合根的判别式即可得出△=8>0,由此可得出该方程有两个不相等的实数根,即A选项不符合题意;B(C)、设方程的两个实数根分别为m、n,根据根与系数的关系即可得出m+n=-2、m•n=-1,由此即可得出B选项不符合题意、C选项符合题意;D、利用公式法求出方程的解,由此即可得出D选项不符合题意.综上即可得出结论.
解答 解:A、∵在方程x2+2x-1=0中,△=22-4×1×(-1)=8>0,
∴该方程有两个不相等的实数根,A选项不符合题意;
B(C)、设方程的两个实数根分别为m、n,
∴m+n=-2,m•n=-1,
∴B选项不符合题意,C选项符合题意;
D、利用公式法可知:x=$\frac{-2±\sqrt{△}}{2}$=-1±$\sqrt{2}$,
∴D选项不符合题意.
故选C.
点评 本题考查了根的判别式、根与系数的关系以及公式法解一元二次方程,逐一分析四个选项的正误是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
19.下列说法中正确的是( )
| A. | 单项式a的系数是0,次数也是0 | |
| B. | 单项式$\frac{-3x}{5}$的系数是-3,次数是1 | |
| C. | 单项式-3×104x2y3的系数是-3,次数是9 | |
| D. | 单项式-5x2y2的系数是-5,次数是4 |
16.已知方程组$\left\{\begin{array}{l}{2x-3y=4}\\{ax+3y=9}\end{array}\right.$ 无解,则a的值是( )
| A. | 2 | B. | -2 | C. | 4.5 | D. | -4.5 |
13. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. |  | B. |  | C. |  | D. |  |
17.下列图形中,不是中心对称图形的是( )
| A. | 平行四边形 | B. | 圆 | C. | 正八边形 | D. | 等边三角形 |


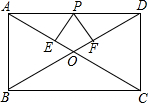 如图,在矩形ABCD中,
如图,在矩形ABCD中, 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.