题目内容
5.关于x的方程-x+k=$\frac{1}{x}$(-2<k<2)的解的个数是0个.分析 根据题目中的方程可转化为一元二次方程,然后根据△的值判断方程根的情况,从而可以解答本题.
解答 解:∵-x+k=$\frac{1}{x}$,
∴x2-kx+1=0,
∴△=(-k)2-4×1×1=k2-4,
∵-2<k<2,
∴△=k2-4<0,
∴关于x的方程-x+k=$\frac{1}{x}$(-2<k<2)的解的个数是0个,
故答案为:0.
点评 本题考查反比例函数、一次函数、一元二次方程,解答此类问题的关键是利用转化的数学思想,将题目中的方程变为一元二次方程,然后根据△的值判断根的情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.△ABC的三边之比为3:4:5,与其相似的△DEF的最短边是9cm,则其最长边的长是( )
| A. | 5 cm | B. | 10 cm | C. | 15 cm | D. | 30 cm |
20.无论a取何值,下列代数式的值总是正数的有( )
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列实数中,属于有理数的是( )
| A. | $\sqrt{2}$ | B. | 1.$\stackrel{•}{4}\stackrel{•}{1}$ | C. | π | D. | $\root{3}{6}$ |
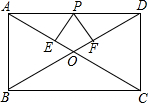 如图,在矩形ABCD中,
如图,在矩形ABCD中, 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.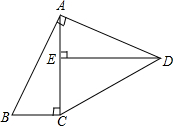 如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.
如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.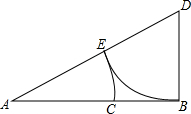 如图,线段AB=2,过点B作BD⊥AB,使BD=$\frac{1}{2}$AB,连接AD,在AD上截取DE=DB.在AB上截取AC=AE.那么线段AC的长为$\sqrt{5}$-1.
如图,线段AB=2,过点B作BD⊥AB,使BD=$\frac{1}{2}$AB,连接AD,在AD上截取DE=DB.在AB上截取AC=AE.那么线段AC的长为$\sqrt{5}$-1.