题目内容
14.若2a+3b=10,其中a≥0,b≥0,又P=5a+2b,求P的取值范围.分析 根据等式的性质,可用a表示b,根据b是非负数,可得a的范围,再根据不等式的性质,可得答案.
解答 解:∵2a+3b=10,
∴b=$\frac{10-2a}{3}$.
∵b≥0,
∴$\frac{10-2a}{3}$≥0,
解得a≤5.
∵a≥0,
∴0≤a≤5.
∵P=5a+2b,
P=5a+2($\frac{10-2a}{3}$)=$\frac{20+11a}{3}$,
∴$\frac{20}{3}$≤P≤25.
点评 本题考查了不等式的性质,用a表示b得出关于a取值范围是解题关键,又利用了不等式的性质1.

练习册系列答案
相关题目
4. 如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )
 如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,则四边形ABCD的面积是( )| A. | 36 | B. | 40 | C. | $\frac{77}{2}$ | D. | 38 |
19.抛物线y=-(x-2)2-3的顶点坐标是( )
| A. | (-2,-3) | B. | (2,3) | C. | (-2,3) | D. | (2,-3) |
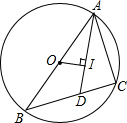 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,求tan∠CAD的值.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,求tan∠CAD的值.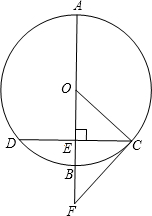 如图,AB是⊙O的直径,弦CD=2$\sqrt{5}$,AB⊥CD于E点,延长AB到F,使得BF=$\frac{1}{2}$OB,连接CF,若CF是⊙O的切线.求:⊙O的半径.
如图,AB是⊙O的直径,弦CD=2$\sqrt{5}$,AB⊥CD于E点,延长AB到F,使得BF=$\frac{1}{2}$OB,连接CF,若CF是⊙O的切线.求:⊙O的半径.