题目内容
4.用简便方法解下列方程组$\left\{\begin{array}{l}{365x+435y=421}\\{435x+365y=379}\end{array}\right.$.
分析 方程组两方程相加求出x+y=1,再利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{365x+435y=421①}\\{435x+365y=379②}\end{array}\right.$,
①+②得:800x+800y=800,即x+y=1③,
①-③×365得:70y=56,即y=$\frac{4}{5}$,
把y=$\frac{4}{5}$代入③得:x=$\frac{1}{5}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{5}}\\{y=\frac{4}{5}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.为了了解某种型号的电风扇的使用寿命,从中抽取30台进行测试,在这个问题中,30台电风扇的使用寿命是( )
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
14.用两种边长相等的正多边形地砖铺地,已有正方形的地砖,还可选择地砖形状为( )
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
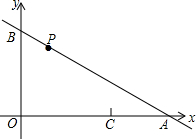 如图所示,在直角坐标系中,直线l与x轴、y轴相交于A、B两点,已知点A的坐标是(8,0),点B的坐标是(0,6).
如图所示,在直角坐标系中,直线l与x轴、y轴相交于A、B两点,已知点A的坐标是(8,0),点B的坐标是(0,6). 如图,点E,F是线段AB的黄金分割点,已知AB=10,求EF的长度.
如图,点E,F是线段AB的黄金分割点,已知AB=10,求EF的长度.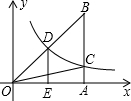 如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.
如图,已知反比例函数的图象经过直角△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为12,求这个反比例函数的解析式.