题目内容
 如图已知,A(a,b),AB⊥y轴于B,且满足
如图已知,A(a,b),AB⊥y轴于B,且满足| a-2 |
(1)求A的坐标;
(2)分别以AB、AO为边作等边△ABC和△AOD,试判断△ACD的形状.
考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:(1)根据算术平方根和偶次方的非负性即可得出方程,求出即可;
(2)证△BAO≌△CAD,推出∠ABO=∠ACD=90°,CD=OB=2=AC,即可得出答案.
(2)证△BAO≌△CAD,推出∠ABO=∠ACD=90°,CD=OB=2=AC,即可得出答案.
解答:解:(1)∵
+(b-2)2=0,
∴a-2=0,b-2=0,
∴a=b=2,
即A的坐标是(2,2);
(2)∵AB⊥y轴,
∴AB=OB=2,∠ABO=90°,
即等边三角形ABC的边长为2,
∴AC=BC=AB=2,
∵以AB、AO为边作等边△ABC和△AOD,
∴AB=AC,AO=AD,∠BAC=∠DAO=60°,
∴∠BAO=∠DAC=60°-∠OAC,
在△BAO和△CAD中
∴△BAO≌△CAD(SAS),
∴CD=OB=2,∠ACD=∠ABO=90°,
∴AC=CD,
即△ACD的形状是等腰直角三角形.
| a-2 |
∴a-2=0,b-2=0,
∴a=b=2,
即A的坐标是(2,2);
(2)∵AB⊥y轴,
∴AB=OB=2,∠ABO=90°,
即等边三角形ABC的边长为2,
∴AC=BC=AB=2,

∵以AB、AO为边作等边△ABC和△AOD,
∴AB=AC,AO=AD,∠BAC=∠DAO=60°,
∴∠BAO=∠DAC=60°-∠OAC,
在△BAO和△CAD中
|
∴△BAO≌△CAD(SAS),
∴CD=OB=2,∠ACD=∠ABO=90°,
∴AC=CD,
即△ACD的形状是等腰直角三角形.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质,坐标与图形性质的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
相关题目
 已知如图,△ACD与△BCE为等腰三角形,其中CA=CD,CB=CE,∠ACD=∠BCE=α,BD、AE交于点F,求∠BFE和∠AFC的度数.
已知如图,△ACD与△BCE为等腰三角形,其中CA=CD,CB=CE,∠ACD=∠BCE=α,BD、AE交于点F,求∠BFE和∠AFC的度数.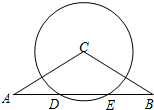 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.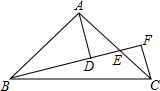 已知Rt△ABC中,AB=AC,∠BAC=90°,E是AC上一点,AD⊥BE于D,CF⊥BE于F,探究AD与DF的关系.
已知Rt△ABC中,AB=AC,∠BAC=90°,E是AC上一点,AD⊥BE于D,CF⊥BE于F,探究AD与DF的关系. 如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.
如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长. 作图:作图题
作图:作图题 在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.
在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.