题目内容
 如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.
如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.考点:平行四边形的性质
专题:
分析:根据平行四边形的对角线互相平分可得OA=
AC=5,OB=
BD=3,由△AOB的周长为15得出AB=7,再根据平行四边形的对边相等,即可求出CD=7.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵四边形ABCD是平行四边形,
∴OA=
AC=5,OB=
BD=3,CD=AB.
∵△AOB的周长为15,
∴OA+OB+AB=5+3+AB=15,
∴AB=7,
∴CD=AB=7.
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∵△AOB的周长为15,
∴OA+OB+AB=5+3+AB=15,
∴AB=7,
∴CD=AB=7.
点评:此题主要考查了平行四边形的性质,用到的知识点:平行四边形的对角线互相平分,平行四边形的两组对边分别相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
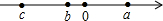 有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )
有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )| A、a、b、c都表示正数 |
| B、b、c为正数,a为负数 |
| C、a、b、c都表示负数 |
| D、b、c为负数,a为正数 |
 如图已知,A(a,b),AB⊥y轴于B,且满足
如图已知,A(a,b),AB⊥y轴于B,且满足 如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时:
如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时: 如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.
如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.