题目内容
 在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.
在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.考点:三角形内角和定理
专题:
分析:先根据∠A=50°求出∠ABC+∠ACB的度数,再根据∠BEC=150°求出∠EBC+∠ECB的度数,由此可得出∠ABE+∠ACE的度数,根据角平分线的性质可得出∠DBE+∠DCE的度数,由三角形内角和定理即可得出结论.
解答:解:∵△ABC中∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°.
∵△BCE中∠E=150°,
∴∠EBC+∠ECB=180°-150°=30°
∴∠ABE+∠ACE=130°-30°=100°.
∵∠ABE的平分线与∠ACE的平分线相交于点D,
∴∠DBE+∠DCE=
(∠ABE+∠ACE)=
×100°=50°,
∴∠DBE+∠DCE=(∠DBE+∠DCE)+(∠EBC+∠ECB)=50°+30°=80°,
∴∠D=180°-80°=100°.
∴∠ABC+∠ACB=180°-50°=130°.
∵△BCE中∠E=150°,
∴∠EBC+∠ECB=180°-150°=30°
∴∠ABE+∠ACE=130°-30°=100°.
∵∠ABE的平分线与∠ACE的平分线相交于点D,
∴∠DBE+∠DCE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBE+∠DCE=(∠DBE+∠DCE)+(∠EBC+∠ECB)=50°+30°=80°,
∴∠D=180°-80°=100°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
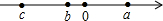 有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )
有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )| A、a、b、c都表示正数 |
| B、b、c为正数,a为负数 |
| C、a、b、c都表示负数 |
| D、b、c为负数,a为正数 |
 如图已知,A(a,b),AB⊥y轴于B,且满足
如图已知,A(a,b),AB⊥y轴于B,且满足 如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.
如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.