Question

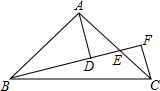已知Rt△ABC中，AB=AC，∠BAC=90°，E是AC上一点，AD⊥BE于D，CF⊥BE于F，探究AD与DF的关系．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：延长AD到G，使DG=CF，连接CG，求出四边形DGCF是矩形，推出DF=CG，证△ADB≌△CGA，推出AD=CG即可．

解答：解：AD=DF，
理由是：延长AD到G，使DG=CF，连接CG，
∵CF⊥BE，AD⊥BE，
∴DG∥CF，∠F=90°，
∴四边形DGCF是矩形，
∴DF=CG，∠G=90°，
∴∠ADB=∠G=90°，
∵∠BAC=90°，
∴∠BAD+∠CAG=90°，∠BAD+∠ABD=90°，
∴∠BAD=∠CAG，
在△ADB和△CGA中

∠ADB=∠G ∠ABD=∠CAG AB=AC

∴△ADB≌△CGA（AAS），
∴AD=CG，
∴AD=DF．

点评：本题考查了全等三角形的性质和判定，矩形的性质和判定，三角形内角和定理的应用，主要考查学生的推理能力．