题目内容
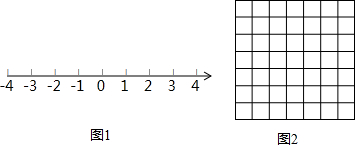 作图:作图题
作图:作图题(1)如图1,在数轴上画出-
| 8 |
(2)图2的正方形网格,每个正方形顶点叫格点,请在图中画一个面积为10的正方形.
考点:勾股定理
专题:作图题
分析:(1)因为8=4+4,则首先作出以2和2为直角边的直角三角形,则其斜边的长即是
.再以原点为圆心,以
为半径画弧,和数轴的负半轴交于一点即可.
(2)面积为10的正方形的边长是
,
是直角边长为1,3的两个直角三角形的斜边长.
| 8 |
| 8 |
(2)面积为10的正方形的边长是
| 10 |
| 10 |
解答: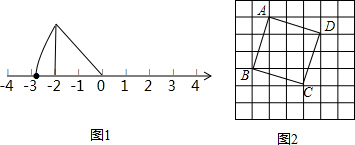 解:(1)因为8=4+4,则首先作出以2和2为直角边的直角三角形,则其斜边的长即是
解:(1)因为8=4+4,则首先作出以2和2为直角边的直角三角形,则其斜边的长即是
,如图1所示:
(2)如图2所示:
∵AB=
=
,
∴S正方形ABCD=
×
=10.
 解:(1)因为8=4+4,则首先作出以2和2为直角边的直角三角形,则其斜边的长即是
解:(1)因为8=4+4,则首先作出以2和2为直角边的直角三角形,则其斜边的长即是| 8 |
,如图1所示:
(2)如图2所示:
∵AB=
| 12+32 |
| 10 |
∴S正方形ABCD=
| 10 |
| 10 |
点评:考查了勾股定理,实数与数轴.能够正确运用数轴上的点来表示一个无理数.(2)解题的关键是找到所求的无理数是直角边长为哪两个有理数的直角三角形的斜边长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
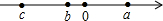 有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )
有理数a,b,c在数轴上位置如图所示,则下列说法正确的是( )| A、a、b、c都表示正数 |
| B、b、c为正数,a为负数 |
| C、a、b、c都表示负数 |
| D、b、c为负数,a为正数 |
 如图已知,A(a,b),AB⊥y轴于B,且满足
如图已知,A(a,b),AB⊥y轴于B,且满足 如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.
如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC. 在△ABC中,∠C=90°,DE⊥AB,BD=BC,若AC=6cm,则AE+DE=
在△ABC中,∠C=90°,DE⊥AB,BD=BC,若AC=6cm,则AE+DE=