题目内容
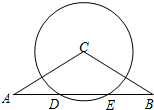 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.(1)求⊙C的半径;
(2)联结CE,求tan∠ECB的值.
考点:垂径定理,勾股定理
专题:
分析:(1)首先过点O作CH⊥DE、垂足为H,连结CD,进而利用锐角三角函数关系以及勾股定理得出AH的长,进而求出DH,AD的长,进而得出答案;
(2)利用锐角三角函数关系得出∠ECB=∠BCH-∠ECH=60°-30°=30°,进而得出答案.
(2)利用锐角三角函数关系得出∠ECB=∠BCH-∠ECH=60°-30°=30°,进而得出答案.
解答: 解:(1)过点O作CH⊥DE、垂足为H,连结CD,
解:(1)过点O作CH⊥DE、垂足为H,连结CD,
∵AC=BC=6,CH⊥AB,
∴∠BCH=∠ACH=
∠ACB=
×120°=60°,
在Rt△ACH中,
∠AHC=90°,cos∠ACH=
,
则CH=AC•cos60°=6×
=3,
故AH=
=
=3
,
∵CH过圆心、CH⊥DE,
∴DH=
DE,
∵DE=AD,
∴EH=DH=
AD,
∴DH=
,AD=2
,
∴CD=
=
=2
;
(2)在Rt△CHE中、∠CHE=90°,
故tan∠ECH=
=
,
则∠ECH=30°,
∵∠BCH=60°,
∴∠ECB=∠BCH-∠ECH=60°-30°=30°,
∴tan∠ECB=tan30°=
.
 解:(1)过点O作CH⊥DE、垂足为H,连结CD,
解:(1)过点O作CH⊥DE、垂足为H,连结CD,∵AC=BC=6,CH⊥AB,
∴∠BCH=∠ACH=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ACH中,
∠AHC=90°,cos∠ACH=
| CH |
| AC |
则CH=AC•cos60°=6×
| 1 |
| 2 |
故AH=
| AC2-CH2 |
| 36-9 |
| 3 |
∵CH过圆心、CH⊥DE,
∴DH=
| 1 |
| 2 |
∵DE=AD,
∴EH=DH=
| 1 |
| 2 |
∴DH=
| 3 |
| 3 |
∴CD=
| CH2+DH2 |
| 9+3 |
| 3 |
(2)在Rt△CHE中、∠CHE=90°,
故tan∠ECH=
| HE |
| CH |
| ||
| 3 |
则∠ECH=30°,
∵∠BCH=60°,
∴∠ECB=∠BCH-∠ECH=60°-30°=30°,
∴tan∠ECB=tan30°=
| ||
| 3 |
点评:此题主要考查了勾股定理以及锐角三角函数关系和垂径定理等知识,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列叙述中,正确的是( )
| A、点A在直线l上 |
| B、直线的一半是射线 |
| C、延长直线AB到C |
| D、射线OA与射线AO是同一条射线 |
 如图已知,A(a,b),AB⊥y轴于B,且满足
如图已知,A(a,b),AB⊥y轴于B,且满足 如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时:
如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时: 如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.
如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC. 如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.
如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.