题目内容
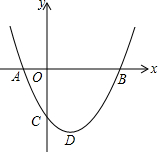 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中:①abc>0;②a+b+c<0;③c+3a=0;④若点M(
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:先根据图象与x轴的交点A,B的横坐标分别为-1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:①∵方程ax2+bx+c=0的两根是-1和3,
∴图象与x轴的交点A,B的横坐标分别为-1,3,
∴对称轴x=-
=1,
∵抛物线的开口方向向上,
∴a>0,
∴b<0
∵抛物线交于y轴负半轴,
∴c<0,
∴abc>0.故选项正确;
②∵对称轴x=1,
∴由图象可知当x=1时,y<0,
∴a+b+c<0.故选项正确;
③∵对称轴x=-
=1,
∴b=-2a,
∴二次函数y=ax2+bx+c(a>0)图象于x的一个交点为(-1,0),
∴a-b+c=0,
∴a+2a+c=0,
即3a+c=0,故选项正确;
④∵对称轴x=1,
∴C(0,c)与对称轴的距离为1,
∵点M(
,m),
∴
-1<1,
∴M与对称轴的距离小于1,
∵抛物线的开口方向向上,
∴m小于c.故选项正确;
故选D.
∴图象与x轴的交点A,B的横坐标分别为-1,3,
∴对称轴x=-
| b |
| 2a |
∵抛物线的开口方向向上,
∴a>0,
∴b<0
∵抛物线交于y轴负半轴,
∴c<0,
∴abc>0.故选项正确;
②∵对称轴x=1,
∴由图象可知当x=1时,y<0,
∴a+b+c<0.故选项正确;
③∵对称轴x=-
| b |
| 2a |
∴b=-2a,
∴二次函数y=ax2+bx+c(a>0)图象于x的一个交点为(-1,0),
∴a-b+c=0,
∴a+2a+c=0,
即3a+c=0,故选项正确;
④∵对称轴x=1,
∴C(0,c)与对称轴的距离为1,
∵点M(
| 2 |
∴
| 2 |
∴M与对称轴的距离小于1,
∵抛物线的开口方向向上,
∴m小于c.故选项正确;
故选D.
点评:考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0;
(2)b由对称轴和a的符号确定:由对称轴公式x=-
判断符号;
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0;
(4)b2-4ac由抛物线与x轴交点的个数确定:
①2个交点,b2-4ac>0;②1个交点,b2-4ac=0;③没有交点,b2-4ac<0.
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0;
(2)b由对称轴和a的符号确定:由对称轴公式x=-
| b |
| 2a |
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0;
(4)b2-4ac由抛物线与x轴交点的个数确定:
①2个交点,b2-4ac>0;②1个交点,b2-4ac=0;③没有交点,b2-4ac<0.

练习册系列答案
相关题目
 如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )
如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )| A、55° | B、60° |
| C、65° | D、70° |
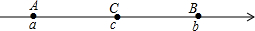 如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )
如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )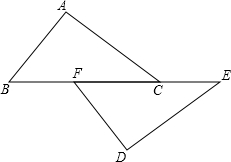 已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.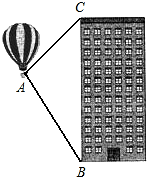 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据: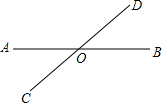 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
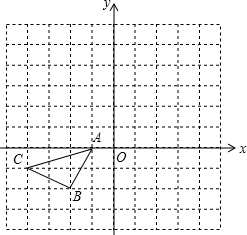 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: