题目内容
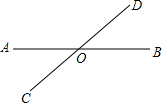 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.(1)求∠BOD的度数;
(2)以O为端点引射线OE、OF,射线OE平分∠BOD,且∠EOF=90°,求∠BOF的度数,并画图加以说明.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据邻补角,可得关于∠BOD的方程,根据解方程,可得答案;
(2)根据角平分线的性质,可得∠BOE的度数,根据角的和差,可得∠BOF的度数.
(2)根据角平分线的性质,可得∠BOE的度数,根据角的和差,可得∠BOF的度数.
解答:解:(1)由邻补角互补,得∠AOD+∠BOD=180°,
即3∠BOD+20°+∠BOD=180°,
解得∠BOD=40°;
(2)如图:
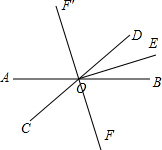
由射线OE平分∠BOD,得
∠BOF=
∠BOD=
×40°=20°,
由角的和差,得∠BOF′=∠EOF′+∠BOE=90°+20°=110°,
∠BOF=∠EOF-∠BOE=90°-20°=70°.
即3∠BOD+20°+∠BOD=180°,
解得∠BOD=40°;
(2)如图:

由射线OE平分∠BOD,得
∠BOF=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠BOF′=∠EOF′+∠BOE=90°+20°=110°,
∠BOF=∠EOF-∠BOE=90°-20°=70°.
点评:本题考查了邻补角,利用邻补角得出关于∠BOD的方程是解题关键,(2)OE⊥OF有两种情况,以防遗漏.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
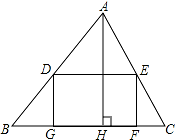 如图,△ABC中,BC=80mm,AH=60mm,D在AB边上,E在AC上,DE∥BC以DE为边在△ABC内作矩形DEFG,设DE=x,DG=y.
如图,△ABC中,BC=80mm,AH=60mm,D在AB边上,E在AC上,DE∥BC以DE为边在△ABC内作矩形DEFG,设DE=x,DG=y.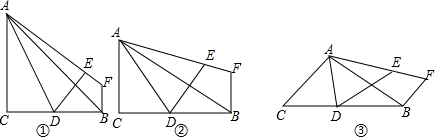
 如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)
如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)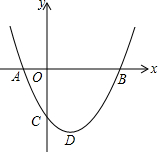 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中: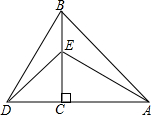 如图,△ACB与△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在BC上,连接AE,BD.
如图,△ACB与△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在BC上,连接AE,BD. 如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.
如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.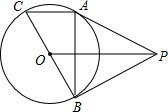 如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:
如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证: