题目内容
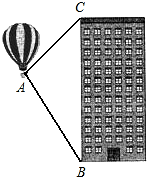 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过A作AD⊥BC,垂足为D,在直角△ABD与直角△ACD中,根据三角函数即可求得BD和CD,即可求解.
解答:解:过A作AD⊥BC,垂足为D.
在Rt△ABD中,
∵∠BAD=60°,AD=30m,
∴BD=AD•tan60°=30×
=30
m,
在Rt△ACD中,
∵∠CAD=30°,AD=30m,
∴CD=AD•tan30°=30×
=10
m,
BC=30
+10
=40
≈68(m).
答:这栋楼高约为68m.
在Rt△ABD中,

∵∠BAD=60°,AD=30m,
∴BD=AD•tan60°=30×
| 3 |
| 3 |
在Rt△ACD中,
∵∠CAD=30°,AD=30m,
∴CD=AD•tan30°=30×
| ||
| 3 |
| 3 |
BC=30
| 3 |
| 3 |
| 3 |
答:这栋楼高约为68m.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据所给的仰角和俯角构造直角三角形,利用三角函数的知识求解直角三角形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
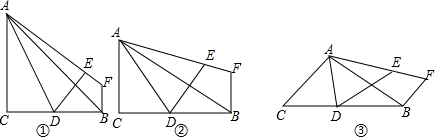
将正方形ABCD的BC边延长到E,使CE=AC,AE与DC相交于点F,则CE:FC=( )
A、2+
| ||
B、
| ||
C、
| ||
D、2-
|
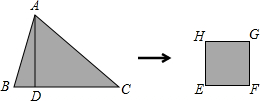 如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )
如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )| A、6cm | B、6.8cm |
| C、7.2cm | D、9cm |
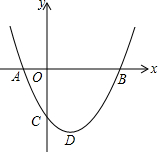 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交于点A、B,与y轴负半轴交于点C,且方程ax2+bx+c=0的两根是-1和3.在下面结论中: 如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠BAD的度数.
如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠BAD的度数. 如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为