题目内容
1.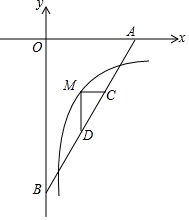 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -6 |
分析 过点D作DE⊥y轴于点E,过点C作CF⊥x轴于点F,然后求出OA与OB的长度,即可求出∠OAB的正弦值与余弦值,再设M(x,y),从而可表示出BD与AC的长度,根据AC•BD=4$\sqrt{3}$列出即可求出k的值.
解答 解:过点D作DE⊥y轴于点E,过点C作CF⊥x轴于点F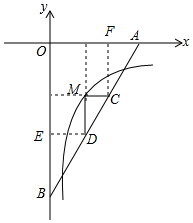 ,
,
令x=0代入y=$\sqrt{3}$x-6,
∴y=-6,
∴B(0,-6),
∴OB=6,
令y=0代入y=$\sqrt{3}$x-6,
∴x=2$\sqrt{3}$,
∴(2$\sqrt{3}$,0),
∴OA=2$\sqrt{3}$,
∴勾股定理可知:AB=4$\sqrt{3}$,
∴sin∠OAB=$\frac{OB}{AB}$=$\frac{\sqrt{3}}{2}$,cos∠OAB=$\frac{OA}{AB}$=$\frac{1}{2}$
设M(x,y),
∴CF=-y,ED=x,
∴sin∠OAB=$\frac{CF}{AC}$,
∴AC=-$\frac{2\sqrt{3}}{3}$y,
∵cos∠OAB=cos∠EDB=$\frac{ED}{BD}$,
∴BD=2x,
∵AC•BD=4$\sqrt{3}$,
∴-$\frac{2\sqrt{3}}{3}$y×2x=4$\sqrt{3}$,
∴xy=-3,
∵M在反比例函数的图象上,
∴k=xy=-3,
故选(A)
点评 本题考查反比例函数与一次函数的综合问题,解题的关键是根据∠OAB的锐角三角函数值求出BD、AC,本题属于中等题型.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12.下列整数中,与$\sqrt{5}$最接近的是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
9.对于二次函数y=x2-2mx-3,下列结论错误的是( )
| A. | 它的图象与x轴有两个交点 | B. | 方程x2-2mx=3的两根之积为-3 | ||
| C. | 它的图象的对称轴在y轴的右侧 | D. | x<m时,y随x的增大而减小 |
6.下列给出的函数中,其图象是中心对称图形的是( )
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
①函数y=x;②函数y=x2;③函数y=$\frac{1}{x}$.
| A. | ①② | B. | ②③ | C. | ①③ | D. | 都不是 |
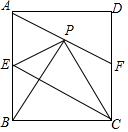 如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).
如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).