题目内容
9.对于二次函数y=x2-2mx-3,下列结论错误的是( )| A. | 它的图象与x轴有两个交点 | B. | 方程x2-2mx=3的两根之积为-3 | ||
| C. | 它的图象的对称轴在y轴的右侧 | D. | x<m时,y随x的增大而减小 |
分析 直接利用二次函数与x轴交点个数、二次函数的性质以及二次函数与方程之间关系分别分析得出答案.
解答 解:A、∵b2-4ac=(2m)2+12=4m2+12>0,
∴二次函数的图象与x轴有两个交点,故此选项正确,不合题意;
B、方程x2-2mx=3的两根之积为:$\frac{c}{a}$=-3,故此选项正确,不合题意;
C、m的值不能确定,故它的图象的对称轴位置无法确定,故此选项错误,符合题意;
D、∵a=1>0,对称轴x=m,
∴x<m时,y随x的增大而减小,故此选项正确,不合题意;
故选:C.
点评 此题主要考查了抛物线与x轴的交点以及二次函数的性质、根与系数的关系等知识,正确掌握二次函数的性质是解题关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 将一组数据中的每一个数据都加同一个正数,方差变大 | |
| B. | 为了解全市同学对书法课的喜欢情况,调查了某校所有女生 | |
| C. | “任意画出一个矩形,它是轴对称图形”是必然事件 | |
| D. | 为了审核书稿中的错别字,选择抽样调查 |
14. 有一个外包装盒为正六棱柱体(如图),它的左视图是( )
有一个外包装盒为正六棱柱体(如图),它的左视图是( )
 有一个外包装盒为正六棱柱体(如图),它的左视图是( )
有一个外包装盒为正六棱柱体(如图),它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
1.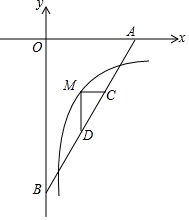 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -6 |
18.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.下面每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 6,8,10 | C. | 3,4,5 | D. | 5,12,13 |
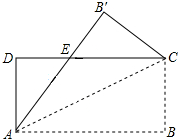 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.