题目内容
13.求不等式组$\left\{\begin{array}{l}{3-x<2x+10}\\{\frac{x}{2}-1≤\frac{x-2}{3}}\end{array}\right.$的所有整数解的和.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式3-x<2x+10,得:x>-$\frac{7}{3}$,
解不等式$\frac{x}{2}$-1≤$\frac{x-2}{3}$,得:x≤2,
则不等式组的解集为-$\frac{7}{3}$<x≤2,
∴该不等式组的所有整数解得和为-2-1+0+1+2=0.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
3.有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x-3|,则其结果恰为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
1.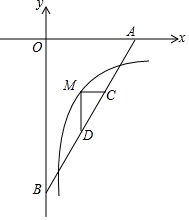 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -6 |
18.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2. 如图所示,所给的三视图表示的几何体是( )
如图所示,所给的三视图表示的几何体是( )
 如图所示,所给的三视图表示的几何体是( )
如图所示,所给的三视图表示的几何体是( )| A. | 圆锥 | B. | 正三棱锥 | C. | 正四棱锥 | D. | 正三棱柱 |
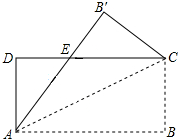 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
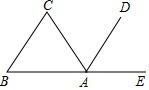 如图,已知A、B、E三点在同一直线上,直线AD平分角∠EAC,AD∥BC,∠B=60°,求∠C的度数.
如图,已知A、B、E三点在同一直线上,直线AD平分角∠EAC,AD∥BC,∠B=60°,求∠C的度数.