题目内容
16.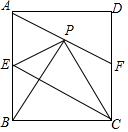 如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).
如图,在矩形ABCD中,点E为AB中点,连接EC,点P是点B关于直线EC的对称点,连结AP并延长交CD于点F,给出下列结论:①AF∥EC;②PE=DF;③若△PBC是等边三角形,则EC=AB;④若AB=30,BC=20,则AP=17.其中正确的结论有①②③.(把所有正确结论的序号都填上).
分析 ①根据三角形内角和为180°易证∠PAB+∠PBA=90°,即可解题;
②易证四边形AECF是平行四边形,即可解题;
③只需证明△PCE≌△PBA即可;
④易证△BEG∽△BCE,即可求得EG的长度,再根据EG是△ABP的中位线即可解题.
解答 解:如图,EC,BP交于点G;
①∵点P是点B关于直线EC的对称点,
∴EC垂直平分BP,
∴EP=EB,
∴∠EBP=∠EPB,
∵点E为AB中点,
∴AE=EB,
∴AE=EP,
∴∠PAB=∠PBA,
∵∠PAB+∠PBA+∠APB=180°,即∠PAB+∠PBA+∠APE+∠BPE=2(∠PAB+∠PBA)=180°,
∴∠PAB+∠PBA=90°,
∴AP⊥BP,
∴AF∥EC;①正确;
②∵AF∥EC,AE∥CF,
∴四边形AECF是平行四边形,
∴CF=AE,
∵AE=PE,∴PE=DF;②正确;
③∵△PBC是等边三角形,
∴∠PBC=∠PCB=60°,PB=PC,
∴∠PBA=30°,
∵EC垂直平分BP,
∴△BCE≌△PCE,
∴∠PCE=30°,∠EPC=∠EBC=90°,
∵在△PCE和△PBA中,$\left\{\begin{array}{l}{∠PBA=∠PCE=30°}\\{PB=PC}\\{∠APB=∠EPC=90°}\end{array}\right.$,
∴△PCE≌△PBA,
∴EC=AB;③正确;
④∵点E为AB中点,AB=30,BC=20,
∴AE=BE=15,EC=$\sqrt{{EB}^{2}{+BC}^{2}}$=25,
∵EC垂直平分BP,
∴△BEG∽△BCE,
∴$\frac{EG}{EB}$=$\frac{BE}{EC}$=$\frac{3}{5}$,∴EG=9;
∵EC∥AF,点E为AB中点,
∴EG是△ABP的中位线,
∴AP=2EG=18,④错误;
故答案为 ①②③.
点评 本题考查了全等三角形的判定和性质,考查了相似三角形的判定和对应边比例相等的性质,本题中找出相似三角形是解题的关键.

| A. | 584×108 | B. | 58.4×109 | C. | 5.84×1010 | D. | 5.84×1011 |
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1128 |
(2)求出商品A,B的原标价.
(3)若商品A、B打折后的价格分别为原价的x%,y%(x、y均为10的整数倍),则按此优惠标准,小林一次性购买这三次商品的总费用比全部按原标价购买优惠1524元.
 某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )
某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )| A. | 40% | B. | 70% | C. | 76% | D. | 96% |
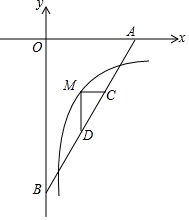 如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )
如图,直线y=$\sqrt{3}$x-6分别交x轴,y轴于A,B,M是反比例函数y=$\frac{k}{x}$(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4$\sqrt{3}$,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -6 |
| A. | $\frac{1}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{4}$ | D. | 3.14 |
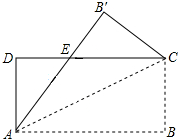 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则△EB′C的周长为11.