题目内容
把二次函数y=x2+kx+c的图象经过(1,0)与(2,5)两点.
(1)求这个函数的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)求抛物线的顶点坐标和对称轴.
(1)求这个函数的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)求抛物线的顶点坐标和对称轴.
考点:抛物线与x轴的交点,二次函数的性质,待定系数法求二次函数解析式
专题:
分析:(1)把(1,0)与(2,5)两点的坐标分别代入函数解析式,列出关于k、c的方程组,通过解方程组来求它们的值;
(2)抛物线与x轴的交点的纵坐标等于零,与y轴交点的横坐标等于零;
(3)通过配方法把二次函数解析式化为顶点式,然后根据解析式直接写出答案.
(2)抛物线与x轴的交点的纵坐标等于零,与y轴交点的横坐标等于零;
(3)通过配方法把二次函数解析式化为顶点式,然后根据解析式直接写出答案.
解答:解:(1)∵二次函数y=x2+kx+c的图象经过(1,0)与(2,5)两点,
∴
,
解得,
,
∴该函数的解析式是:y=x2+2x-3;
(2)∵由(1)知,该函数的解析式是y=x2+2x-3,则y=(x+3)(x-1).
∴当x=0时,y=-3,即该函数图象与y轴交于点(0,-3).
又∵y=x2+2x-3=(x+3)(x-1),
∴该函数图象与x轴交于点(-3,0)和(1,0);
(3)∵y=x2+2x-3=(x+1)2-7,即抛物线的解析式是y=(x+1)2-7,
∴抛物线的顶点坐标是(-1,-7),对称轴是x=-1.
∴
|
解得,
|
∴该函数的解析式是:y=x2+2x-3;
(2)∵由(1)知,该函数的解析式是y=x2+2x-3,则y=(x+3)(x-1).
∴当x=0时,y=-3,即该函数图象与y轴交于点(0,-3).
又∵y=x2+2x-3=(x+3)(x-1),
∴该函数图象与x轴交于点(-3,0)和(1,0);
(3)∵y=x2+2x-3=(x+1)2-7,即抛物线的解析式是y=(x+1)2-7,
∴抛物线的顶点坐标是(-1,-7),对称轴是x=-1.
点评:本题考查了待定系数法求二次函数的解析,抛物线与x轴的交点.解题时,需要熟悉二次函数的三种解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
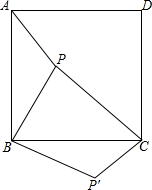 如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上.
如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上.