题目内容
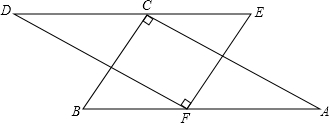
将两块大小相同的直角三角尺(△ABC和△DEF,其中∠A=∠D=30°)按如图所示的位置摆放(直角顶点F在斜边AB上,直角顶点C在斜边DE上),且DE∥AB.
(1)求∠ACD的度数;
(2)问:DF与AC平行吗?说明你的理由.
(1)求∠ACD的度数;
(2)问:DF与AC平行吗?说明你的理由.

考点:平行线的判定与性质
专题:
分析:(1)根据两直线平行,同旁内角互补求解即可;
(2)根据两直线平行,内错角相等求出∠ACE,再然后利用同位角相等,两直线平行证明即可.
(2)根据两直线平行,内错角相等求出∠ACE,再然后利用同位角相等,两直线平行证明即可.
解答: (1)解:∵DE∥AB,
(1)解:∵DE∥AB,
∴∠ACD=180°-∠A=180°-30°=150°;
(2)解:DF∥AC.
理由如下:∵DE∥AB,
∴∠ACE=∠A=30°,
∵∠D=30°,
∴∠ACE=∠D,
∴DF∥AC.
 (1)解:∵DE∥AB,
(1)解:∵DE∥AB,∴∠ACD=180°-∠A=180°-30°=150°;
(2)解:DF∥AC.
理由如下:∵DE∥AB,
∴∠ACE=∠A=30°,
∵∠D=30°,
∴∠ACE=∠D,
∴DF∥AC.
点评:本题考查了平行线的判定与性质,直角三角板的性质,熟记平行线的判定方法和性质是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
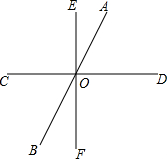 如图,直线AB、CD、EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,
如图,直线AB、CD、EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4, 如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.
如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.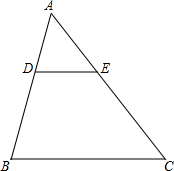 如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.
如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.