题目内容
13. 如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中,满足哪两个条件可判定△OBC是等腰三角形(请用条件前的序号写出所有情形);
(2)请选择(1)中的一种情形说明理由.
分析 (1)可以利用三角形全等的判定方法解决问题.
(2)有两种情形,只要证明△BEO≌△CDO即可解决.
解答 解:(1)①③或②③
(2)满足①③时,
在△BEO和△CDO中,
$\left\{\begin{array}{l}{∠EBO=∠DCO}\\{∠EOB=∠DOC}\\{BE=CD}\end{array}\right.$,
∴△BEO≌△CDO,
∴OB=OC,
∴△OBC是等腰三角形.
满足②③时,
在△BEO和△CDO中,
$\left\{\begin{array}{l}{∠BEO=∠CDO}\\{∠EOB=∠DOC}\\{BE=CD}\end{array}\right.$,
∴△BEO≌△CDO,
∴OB=OC,
∴△OBC是等腰三角形.
点评 本题考查全等三角形的判定和性质,解题的关键是首先理解题意,其次是正确寻找哪两个三角形全等.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.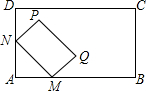 如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
 如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )| A. | 4 | B. | 2$\sqrt{13}$ | C. | 7 | D. | 8 |

 如图,在四边形ABCD中,对角线AC,BD交于点E,AE=2,CE=3,AB=2,D到AC的距离为1,求四边形ABCD的面积.
如图,在四边形ABCD中,对角线AC,BD交于点E,AE=2,CE=3,AB=2,D到AC的距离为1,求四边形ABCD的面积.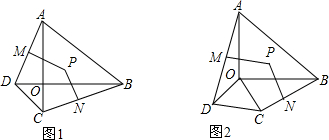
 小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,
小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,