题目内容
8.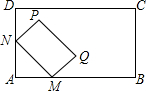 如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )| A. | 4 | B. | 2$\sqrt{13}$ | C. | 7 | D. | 8 |
分析 如图所示,取MN中点E,当点A、E、P三点共线时,AP最大,利用勾股定理及直角三角形中斜边上的中线等于斜边的一半分别求出PE与AE的长,由AE+EP求出AP的最大值即可.
解答 解:如图所示,取MN中点E,当点A、E、P三点共线时,AP最大,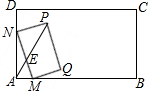
在Rt△PNE中,PN=4,NE=$\frac{1}{2}$MN=3,
根据勾股定理得:PE=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△AMN中,AE为斜边MN上的中线,
∴AE=$\frac{1}{2}$MN=3,
则AP的最大值为AE+EP=5+3=8.
故选D.
点评 此题考查了勾股定理,直角三角形斜边上的中线性质,以及矩形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.下列函数中,y是x的反比例函数的是( )
| A. | y=3x | B. | y-3=2x | C. | xy=1 | D. | y=x2 |
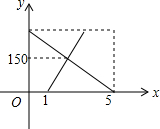 一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.
一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇. 如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件: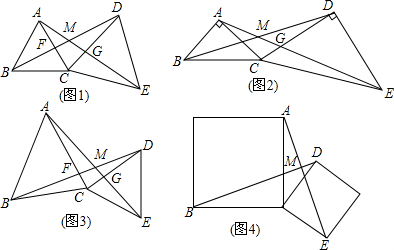
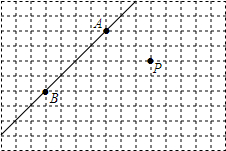 在如图所示的方格纸上,只用直尺画图.
在如图所示的方格纸上,只用直尺画图. 如图,已知△ABC,请作出△ABC关于x轴对称的图形.并写出A、B、C关于x轴对称的点坐标.
如图,已知△ABC,请作出△ABC关于x轴对称的图形.并写出A、B、C关于x轴对称的点坐标.