题目内容
14．若二次函数y=x2+3x+e（e为整数）的图象与x轴没有交点，则e的最小值是3．分析 根据二次函数的性质得出△=b2-4ac=32-4×1×e=9-4e＜0，进而得出答案．
解答 解：∵二次函数y=x2+3x-+e（e为整数）的图象与x轴没有交点，
∴△=b2-4ac=32-4×1×e=9-4e＜0，
解得：e＞$\frac{9}{4}$，
∵e为整数，
∴e的最小值是3．
故答案为：3．
点评 本题考查二次函数的性质、一元一次不等式的解法，记住△＞0抛物线与x轴有两点交点，△=0抛物线与x轴只有两个交点，△＜0抛物线与x轴没有交点．
练习册系列答案
名校课堂系列答案
相关题目
2．下列各式与$\sqrt{3}$是同类二次根式的是（ ）
| A． | $\sqrt{9}$ | B． | $\sqrt{18}$ | C． | $\sqrt{12}$ | D． | $\sqrt{6}$ |
抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，其部分图象如图所示．已知ax2+bx+c=0的两个根分别为x1、x2，且x1＜x2，则x2的取值范围是0＜x2＜1．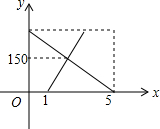
一辆货车从A地出发以一定的速度匀速驶往B地，1小时后，一辆小汽车从B地出发沿同一条路匀速驶往A地，结果小汽车比货车早1小时达到目的地，两车离B地的距离y（km）与所用时间x（h）的函数关系如图所示，则小汽车出发1.5小时后与货车相遇．
如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列三个条件：