题目内容
2. 小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,
小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,在主持节目时,主持人站在舞台的黄金分割点处最自然得体,那么在长20米的舞台AB上,主持人从A点到B点走多少米,他的站台最得体?(取$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{5}$=2.2)
分析 设AC=x米,根据把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,列出方程求解即可.
解答 解:设AC=x米,
∵AB=20,
∴BC=(20-x)米,
∴(20-x)2=x•20,
解得:x1=10$\sqrt{5}$-10=12,x2=30-10$\sqrt{5}$=8,
∴AB=12米或8米,
答:主持人从A点到B点走12米或8米他的站台最得体.
点评 此题考查了理解黄金分割,找出黄金分割中成比例的对应线段列出方程是解决问题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.下列各式与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{18}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
 如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
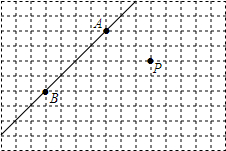 在如图所示的方格纸上,只用直尺画图.
在如图所示的方格纸上,只用直尺画图. 一般地,y=$\frac{k}{x+a}$与y=$\frac{k}{x}$的图象的形状、大小均完全相同,把函数y=$\frac{k}{x}$的图象进行适当的平移就可以得到y=$\frac{k}{x+a}$的图象.已知y=$\frac{1}{x}$与y=$\frac{1}{x-2}$在同一坐标系中的图象如图所示,则不等式$\frac{1}{x-2}>\frac{1}{x}$的解集为( )
一般地,y=$\frac{k}{x+a}$与y=$\frac{k}{x}$的图象的形状、大小均完全相同,把函数y=$\frac{k}{x}$的图象进行适当的平移就可以得到y=$\frac{k}{x+a}$的图象.已知y=$\frac{1}{x}$与y=$\frac{1}{x-2}$在同一坐标系中的图象如图所示,则不等式$\frac{1}{x-2}>\frac{1}{x}$的解集为( )