题目内容
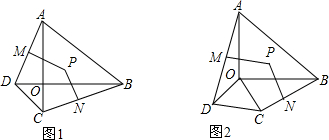
5.已知在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°(1)如图1,若D、O、B在一条直线上,连接AD、BC,取AD、BC的中点M、N,MP⊥AD,NP⊥BC,MP、NP相交于P,则PM+PN与AD+BC之间有何确定的关系?直接写出结果;
(2)如图2,将△OCD绕O旋转,则(1)中的结论是否变化,请说明理由.
分析 (1)要证明AD+BC=2(PM+PN),只要证明AD=2PM,BC=2PN,只要证明∠APD=90°利用“8字型”即可证明.
(2)由△AOC≌△BOD得∠OAC=∠OBD结合“8字型”证明AC⊥BD,再由△APC≌△DPB得∠1=∠2结合“8字型”即可证明∠APD=90°.
解答 (1)结论:AD+BC=2(PM+PN).理由如下: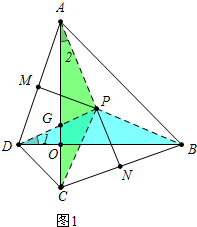
证明:连接PA、PD、PC、PB.
∵PM垂直平分AD,PN垂直平分BC,
∴PA=PD,PC=PB,
∵OA=OB,OD=OC,
∴AC=BD,
在△APC和△DPB中,
$\left\{\begin{array}{l}{PA=PD}\\{PC=PB}\\{AC=BD}\end{array}\right.$,
∴△APC≌△DPB,
∴∠1=∠2,
∵∠1+∠DGO=90°,∠DGO=∠AGP,
∴∠2+∠AGP=90°
∴∠APD=90°,
∵AM=MD,
∴PM=$\frac{1}{2}$AD,同理PN=$\frac{1}{2}BC$,
∴AD+BC=2(PM+PN).
(2)如图2中,连接AC、BD、PA、PD、PB、PC,AC分别与PD、OB、BD交于点G、K、H.
∵∠AOB=∠DOC=90°,
∴∠AOC=∠DOB,
在△AOC或△BOD中,
$\left\{\begin{array}{l}{AO=BO}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,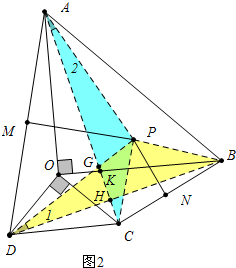
∴△AOC≌△BOD,
∴AC=BD,∠OAC=∠OBD,
∵∠OAK+∠AKO=90°,∠AKO=∠BKH,
∴∠BKH+∠KBH=90°,
∴∠KHB=∠KHD=90°,
∵PM垂直平分AD,PN垂直平分BC
∴PA=PD,PC=PB,
在△APC和△DPB中,
$\left\{\begin{array}{l}{PA=PD}\\{PC=PB}\\{AC=BD}\end{array}\right.$,
∴△APC≌△DPB,
∴∠1=∠2,
∵∠1+∠DGH=90°,∠DGH=∠AGP,
∴∠2+∠AGP=90°
∴∠APD=90°,
∵AM=MD,
∴PM=$\frac{1}{2}$AD,同理PN=$\frac{1}{2}BC$,
∴AD+BC=2(PM+PN).
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、等角的余角相等,关键是添加辅助线构造全等三角形,巧妙利用“8字型”证明直角.

 阅读快车系列答案
阅读快车系列答案| A. | 1.425×108 | B. | 1.425×107 | C. | 14.25×106 | D. | 1425×104 |
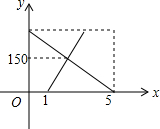 一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇.
一辆货车从A地出发以一定的速度匀速驶往B地,1小时后,一辆小汽车从B地出发沿同一条路匀速驶往A地,结果小汽车比货车早1小时达到目的地,两车离B地的距离y(km)与所用时间x(h)的函数关系如图所示,则小汽车出发1.5小时后与货车相遇. 如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件:
如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列三个条件: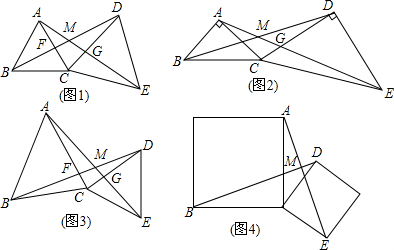

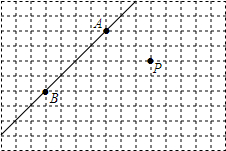 在如图所示的方格纸上,只用直尺画图.
在如图所示的方格纸上,只用直尺画图.