题目内容
9. 补充并完成下列证明:
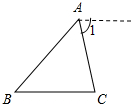
补充并完成下列证明:已知:如图,△ABC,
求证:∠A+∠B+∠C=180°.
证明:过点A作AD∥BC,
∵AD∥BC,(已知)
∴∠BAC+∠1+∠B=180°(两直线平行,同旁内角互补)
而∠1=∠C,(两直线平行,内错角相等)
∴∠A+∠B+∠C=180°.(等量代换)
分析 过点A作AD∥BC,再根据平行线的性质可得到∠BAC+∠1+∠B=180°,∠1=∠C,从而证得∠A+∠B+∠C=180°,据此填空即可.
解答 证明:过点A作AD∥BC,
∵AD∥BC,(已知)
∴∠BAC+∠1+∠B=180°(两直线平行,同旁内角互补)
而∠1=∠C,(两直线平行,内错角相等)
∴∠A+∠B+∠C=180°.(等量代换),
故答案为:两直线平行,同旁内角互补;两直线平行,内错角相等∴∠A+∠B+∠C=180°,等量代换.
点评 本题主要考查平行线的性质和三角形的内角和定理,掌握平行线的性质是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
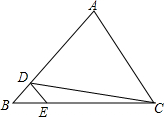 如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( ) 已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.
已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.