题目内容
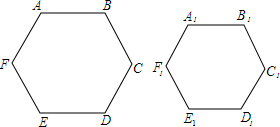
1.如图,正六边形ABCDEF和正六边形A1B1C1D1E1F1相似,AB=4,E1F1=3.(1)求正六边形ABCDEF与正六边形A1B1C1D1E1F1的周长比;
(2)求正六边形ABCDEF与正六边形A1B1C1D1E1F1的面积比.
分析 (1)根据两个正六边形相似,相似多边形的周长的比等于相似比求解;
(2)根据两个正六边形相似,相似多边形的面积的比等于相似比的平方求解.
解答 解:(1)正六边形ABCDEF与正六边形A1B1C1D1E1F1的周长比=AB:E1F1=4:3;
(2)正六边形ABCDEF与正六边形A1B1C1D1E1F1的面积比=(AB:E1F1)2=(4:3)2=16:9.
点评 本题考查了相似三角形的性质,相似三角形周长的比等于相似比,面积的比等于相似比的平方.

练习册系列答案
相关题目
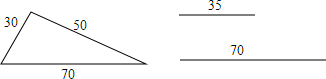
10.x分别取1,2,3,4,5这五个数时,代数式(x-1)(x+2)(x-3)的值为0的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
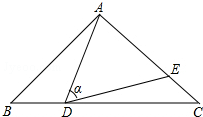 如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),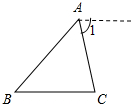 补充并完成下列证明:
补充并完成下列证明: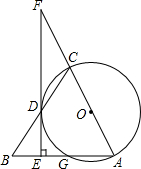 如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.
如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.