题目内容
19.若(2a-3)2与|b+1|互为相反数,求代数式3ab2+4a2b-[5ab2-2(3a2b-1)]的值.分析 先由非负数的性质可求得a=1.5,b=-1,然后再化简代数式,最后求值即可.
解答 解:∵(2a-3)2与|b+1|互为相反数,
∴2a-3)2+|b+1|=0.
∴a=1.5,b=-1.
原式=3ab2+4a2b-[5ab2-6a2b+2]
=3ab2+4a2b-5ab2+6a2b-2
=10a2b-2ab2-2.
将a=1.5,b=-1代入得:
原式=10×1.52×(-1)-2×1.5×(-1)2-2
=-22.5-3-2
=-27.5.
点评 本题主要考查的是整式的加减、非负数的性质,求得a、b的值是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
10.已知$\frac{a}{b}=\frac{2}{3}$,则$\frac{a}{a+b}$( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
7. 如图,已知线段AB=20cm,点N在AB上,AN=4NB,那么线段AN的长为( )
如图,已知线段AB=20cm,点N在AB上,AN=4NB,那么线段AN的长为( )
 如图,已知线段AB=20cm,点N在AB上,AN=4NB,那么线段AN的长为( )
如图,已知线段AB=20cm,点N在AB上,AN=4NB,那么线段AN的长为( )| A. | 10cm | B. | 12cm | C. | 16cm | D. | 18cm |
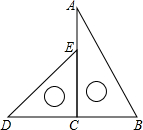 如图,这是一幅由含45°和30°的三角板拼成的图案.
如图,这是一幅由含45°和30°的三角板拼成的图案. 如图,从教室门B到图书馆A,总有一些同学不文明,为了走捷径,不走人行道而横穿草坪,其中包含的数学几何知识为:两点之间线段最短.
如图,从教室门B到图书馆A,总有一些同学不文明,为了走捷径,不走人行道而横穿草坪,其中包含的数学几何知识为:两点之间线段最短.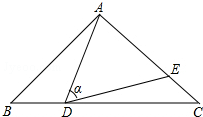 如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合), 已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:
已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求: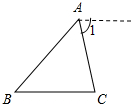 补充并完成下列证明:
补充并完成下列证明: