题目内容
4. 已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.
已知AD为∠BAC的平分线,EF为AD的垂直平分线,求证:FD2=FB•FC.
分析 连结AF,则DF=AF,再由△ACF∽△BAF,对应边成比例,即可求证.
解答  证明:连接AF,
证明:连接AF,
∵AD是角平分线,
∴∠BAD=∠CAD,
又∵EF为AD的垂直平分线,
∴AF=FD,∠DAF=∠ADF,
∴∠DAC+∠CAF=∠B+∠BAD,
∴∠CAF=∠B,
∵∠AFC=∠AFC,
∴△ACF∽△BAF,即$\frac{CF}{AF}$=$\frac{AF}{BF}$,
∴AF2=CF•BF,
即FD2=CF•BF.
点评 本题主要考查了相似三角形的判定及性质以及垂直平分线的性质问题,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
19.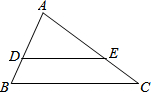 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
 如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积之比是( )| A. | 3:2 | B. | 3:5 | C. | 9:16 | D. | 9:4 |
 如图,从教室门B到图书馆A,总有一些同学不文明,为了走捷径,不走人行道而横穿草坪,其中包含的数学几何知识为:两点之间线段最短.
如图,从教室门B到图书馆A,总有一些同学不文明,为了走捷径,不走人行道而横穿草坪,其中包含的数学几何知识为:两点之间线段最短.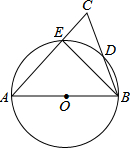 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④. 补充并完成下列证明:
补充并完成下列证明: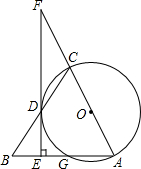 如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.
如图,△ABC中,以AC为直径的⊙O与边BC、BA交于点D、G,D是BC的中点,DE⊥AB,垂足为E,ED与AC的延长线交于点F.
 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.
如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.