题目内容
19.在Rt△ABC中,∠C=90°,BC=AC,AB=8,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是8$\sqrt{2}$-8≤AD<4.分析 以D为圆心,AD的长为半径画圆,当圆与BC相切时,AD最小,与线段BC相交且交点为B或C时,AD最大,分别求出即可得到范围.
解答  解:以D为圆心,AD的长为半径画圆
解:以D为圆心,AD的长为半径画圆
①当圆与BC相切时,DE⊥BC时,
∵BC=AC,
∴∠ABC=45°,
∴DE=$\frac{\sqrt{2}}{2}$BD,
∵AB=8,
∴设AD=DE=x,则DB=8-x,
∴$\frac{\sqrt{2}}{2}$(8-x)=x
∴x=AD=8$\sqrt{2}$-8;
②当圆与BC相交时,若交点为B或C,则AD=$\frac{1}{2}$AB=4,
∴AD的取值范围是8$\sqrt{2}$-8≤AD<4.
故答案为:8$\sqrt{2}$-8≤AD<4.
点评 本题考查了等腰三角形的判定与性质,利用边BC与圆的位置关系解答,分清AD最小和最大的两种情况是解决本题的关键.

练习册系列答案
相关题目
10.x分别取1,2,3,4,5这五个数时,代数式(x-1)(x+2)(x-3)的值为0的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
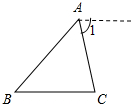 补充并完成下列证明:
补充并完成下列证明: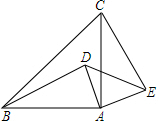 如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.
如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.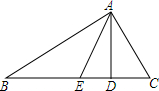 如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.
如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.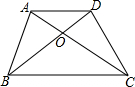 加图,在四边形ABCD中,AD∥BC,AD=1,BC=3,那么S△AOD:S四边形ABCD的值为多少?
加图,在四边形ABCD中,AD∥BC,AD=1,BC=3,那么S△AOD:S四边形ABCD的值为多少?