题目内容
20.已知$\sqrt{a}$+$\sqrt{b}$=1,且$\sqrt{a}$=m+$\frac{a-b}{2}$,$\sqrt{b}$=n-$\frac{a-b}{2}$,其中m、n均为有理数,求m2+n2的值.分析 由$\sqrt{a}$=m+$\frac{a-b}{2}$,$\sqrt{b}$=n-$\frac{a-b}{2}$,把a-b利用平方差公式因式分解,整理求得m、n,代入求得答案即可.
解答 解:∵$\sqrt{a}$+$\sqrt{b}$=1,$\sqrt{a}$=m+$\frac{a-b}{2}$,$\sqrt{b}$=n-$\frac{a-b}{2}$,
∴m=$\sqrt{a}$-$\frac{a-b}{2}$=$\sqrt{a}$-$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{2}$=$\sqrt{a}$-$\frac{\sqrt{a}-\sqrt{b}}{2}$=$\frac{\sqrt{a}+\sqrt{b}}{2}$=$\frac{1}{2}$,
n=$\sqrt{b}$+$\frac{a-b}{2}$=$\sqrt{b}$+$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{2}$=$\sqrt{b}$+$\frac{\sqrt{a}-\sqrt{b}}{2}$=$\frac{\sqrt{a}+\sqrt{b}}{2}$=$\frac{1}{2}$,
∴m2+n2=$\frac{1}{4}$+$\frac{1}{4}$=$\frac{1}{2}$.
点评 此题考查二次根式的化简求值,利用平方差公式因式分解是解决问题的关键.

练习册系列答案
相关题目
10.已知$\frac{a}{b}=\frac{2}{3}$,则$\frac{a}{a+b}$( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
10.x分别取1,2,3,4,5这五个数时,代数式(x-1)(x+2)(x-3)的值为0的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
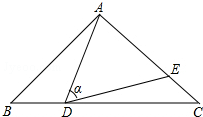 如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合), 已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:
已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求: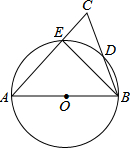 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.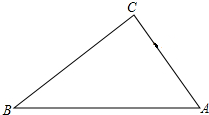 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒. 补充并完成下列证明:
补充并完成下列证明: