题目内容
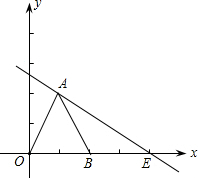 如图,△OAB是边长为2的等边三角形,过点A的直线y=-
如图,△OAB是边长为2的等边三角形,过点A的直线y=-
| ||
| 3 |
(1)求点E的坐标.
(2)求证:OA⊥AE.
考点:一次函数图象上点的坐标特征,等边三角形的性质
专题:
分析:(1)利用等边三角形的性质得出OD=BD=1,再利用勾股定理得出AD的长,即可得出A点坐标,即可求出函数解析式;
(2)利用E点坐标得出EO的长,进而求出AE的长,再利用勾股定理逆定理得出答案.
(2)利用E点坐标得出EO的长,进而求出AE的长,再利用勾股定理逆定理得出答案.
解答: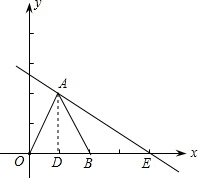 (1)解:过点A作AD⊥EO于点D,
(1)解:过点A作AD⊥EO于点D,
∵△OAB是边长为2的等边三角形,
∴OD=DB=1,AB=AO=OB=2,
∴AD=
,
∴A(1,
),
将A点代入直线y=-
x+m得:
=-
+m,
解得:m=
,
故y=-
x+
,
则y=0时,x=4,
即E(4,0);
(2)证明:∵AD=
,DE=EO-DO=3,
∴AE=
=2
,
∵AO2+AE2=16,EO2=16,
∴AO2+AE2=EO2,
∴OA⊥AE.
 (1)解:过点A作AD⊥EO于点D,
(1)解:过点A作AD⊥EO于点D,∵△OAB是边长为2的等边三角形,
∴OD=DB=1,AB=AO=OB=2,
∴AD=
| 3 |
∴A(1,
| 3 |
将A点代入直线y=-
| ||
| 3 |
| 3 |
| ||
| 3 |
解得:m=
4
| ||
| 3 |
故y=-
| ||
| 3 |
4
| ||
| 3 |
则y=0时,x=4,
即E(4,0);
(2)证明:∵AD=
| 3 |
∴AE=
32+(
|
| 3 |
∵AO2+AE2=16,EO2=16,
∴AO2+AE2=EO2,
∴OA⊥AE.
点评:此题主要考查了等边三角形的性质以及勾股定理以及勾股定理逆定理和一次函数图象上点的坐标性质,得出A点坐标是解题关键.

练习册系列答案
相关题目
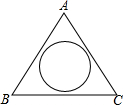 如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.
如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.