题目内容
如图：在正三角形ABC中，AB=BC=AC=4，则点A的坐标为考点：等边三角形的性质,坐标与图形性质
专题：
分析：由AO⊥BC，且AB=AC=4直接得到BO=CO=2，进而运用勾股定理求出AO的长度，问题即可解决．
解答：解：∵AO⊥BC，且AB=AC=4，
∴BO=CO=2；
由勾股定理得：
AO2=AB2-BO2=16-4=12，
∴AO=2
，
∴点A的坐标为（0，2
），
故答案为：（0，2
）．
解：∵AO⊥BC，且AB=AC=4，∴BO=CO=2；
由勾股定理得：
AO2=AB2-BO2=16-4=12，
∴AO=2
| 3 |
∴点A的坐标为（0，2
| 3 |
故答案为：（0，2
| 3 |
点评：该命题以直角坐标系为载体，以等边三角形的性质及图形与坐标的关系的考查为核心构造而成；解题的关键是灵活运用有关定理来分析或解答．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
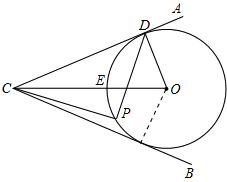如图：∠ACB=60°，CE平分∠ACB，O为射线CE上的一点，⊙O切AC于点D
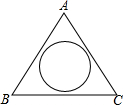如图，在一块三角形空地中间建一个圆形花圃，测得该三角形空地的AB边长为12米，BC边长为14米，∠ABC=52°，圆形花圃的半径为3米，求余下空地的面积．
如图，已知A，B，C，D是⊙O上的四个点，AB=BC，BD交AC于点E，连结CD
如图，等腰梯形ABCD中，AD∥BC，将其中一条对角线BD平移到CE的位置，则：