题目内容
如图6,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上1、2、3、4四个数字;转盘B被均匀分成6等份,每份标上1、2、3、4、5、6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
(1)同时转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲胜;如果所得的积是奇数,那么乙胜.你认为这样的规则是否公平?请你说明理由.

(1)同时转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲胜;如果所得的积是奇数,那么乙胜.你认为这样的规则是否公平?请你说明理由.
考点:游戏公平性,列表法与树状图法
专题:
分析:首先根据题意画出树状图,然后根据树状图即可求得甲乙获胜的概率,因为概率不等,可求得得分也不等,故不公平.新游戏规则,只要能求得甲乙得分相等即可.
解答:解:不公平.
画树状图得:
∵共有24种等可能的结果,所得的积是偶数的有18种情况,是奇数的有6种情况,
∴P(甲获胜)=
=
,P(乙获胜)=
=
,
∴不公平.

画树状图得:
∵共有24种等可能的结果,所得的积是偶数的有18种情况,是奇数的有6种情况,
∴P(甲获胜)=
| 18 |
| 24 |
| 3 |
| 4 |
| 6 |
| 24 |
| 1 |
| 4 |
∴不公平.
点评:本题考查的是游戏公平性的判断.注意解此题的关键是计算每个事件的概率,然后根据概率求得甲乙的得分,比较得分即可判定是否公平.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图所示,已知AC=BD,∠CAB=∠DBA.求证:
如图所示,已知AC=BD,∠CAB=∠DBA.求证: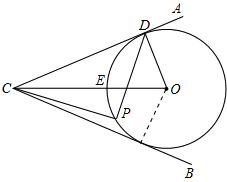 如图:∠ACB=60°,CE平分∠ACB,O为射线CE上的一点,⊙O切AC于点D
如图:∠ACB=60°,CE平分∠ACB,O为射线CE上的一点,⊙O切AC于点D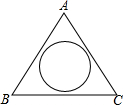 如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.
如图,在一块三角形空地中间建一个圆形花圃,测得该三角形空地的AB边长为12米,BC边长为14米,∠ABC=52°,圆形花圃的半径为3米,求余下空地的面积.