题目内容
12.(1)计算:2$\sqrt{1\frac{1}{2}}$÷$\sqrt{\frac{3}{4}}$-(2-$\sqrt{2}$)2(2)解方程组:$\left\{\begin{array}{l}{2x+y=5}\\{x-3y=6}\end{array}\right.$.
分析 (1)先利用二次根式的除法法则和完全平方公式计算,然后合并即可;
(2)先利用加减消元法求出y的值,然后利用代入法求出x的值,从而得到方程组的解.
解答 解:(1)原式=2$\sqrt{\frac{3}{2}×\frac{4}{3}}$-(4-4$\sqrt{2}$+2)
=2$\sqrt{2}$-6+4$\sqrt{2}$
=6$\sqrt{2}$-6;
(2)$\left\{\begin{array}{l}{2x+y=5①}\\{x-3y=6②}\end{array}\right.$,
①-②×2得y+6y=5-12,
解得y=-1,
把y=-1代入②得x-3×(-1)=6,
解得x=3,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
2.将抛物线y=x2-2x+3向右平移2个单位长度,再向上平移3个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x+1)2+5 | B. | y=(x-4)2+4 | C. | y=(x+2)2+4 | D. | y=(x-3)2+5 |
17.估计$\sqrt{15}$的值在( )
| A. | 1与2之间 | B. | 2与3之间 | C. | 3与4之间 | D. | 4与5之间 |
2.现规定一种新的运算“*”:a*b=ab.如2*3=23=8,那么$({-\frac{1}{2}})$*3=( )
| A. | $\frac{1}{8}$ | B. | -8 | C. | $-\frac{1}{8}$ | D. | $-\frac{3}{2}$ |
 如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.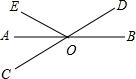 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠AOE=50°,∠EOD=80°.
如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠AOE=50°,∠EOD=80°.