题目内容
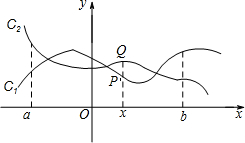
19.如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.(1)判断函数y=3x+2与y=2x+1在-2≤x≤0上是否为“相邻函数”,并说明理由;
(2)若函数y=x2-x与y=x-a在0≤x≤2上是“相邻函数”,求a的取值范围;
(3)若函数y=$\frac{a}{x}$与y=-2x+4在1≤x≤2上是“相邻函数”,直接写出a的最大值与最小值.
分析 (1)直接利用相邻函数的定义结合一次函数增减性,得出当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1,进而判断即可;
(2)直接利用相邻函数的定义结合二次函数增减性,得出当x=1时,函数有最小值a-1,当x=0或x=2时,函数有最大值a,即a-1≤y≤a,进而判断即可;
(3)直接利用相邻函数的定义结合函数增减性,得出当x=1时,函数有最小值a-2,当x=2时,函数有最大值$\frac{a}{2}$,即a-2≤y≤$\frac{a}{2}$,进而判断最值即可.
解答 解:(1)是“相邻函数”,
理由如下:y1-y2=(3x+2)-(2x+1)=x+1,构造函数y=x+1,
∵y=x+1在-2≤x≤0,是随着x的增大而增大,
∴当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1,
∴-1≤y1-y2≤1,
即函数y=3x+2与y=2x+1在-2≤x≤0上是“相邻函数”;
(2)y1-y2=(x2-x)-(x-a)=x2-2x+a,构造函数y=x2-2x+a,
∵y=x2-2x+a=(x-1)2+(a-1),
∴顶点坐标为:(1,a-1),
又∵抛物线y=x2-2x+a的开口向上,
∴当x=1时,函数有最小值a-1,当x=0或x=2时,函数有最大值a,即a-1≤y≤a,
∵函数y=x2-x与y=x-a在0≤x≤2上是“相邻函数”,
∴-1≤y1-y2≤1,即$\left\{\begin{array}{l}{a≤1}\\{a-1≥-1}\end{array}\right.$,
∴0≤a≤1;
(3)y1-y2=$\frac{a}{x}$-(-2x+4)=$\frac{a}{x}$+2x-4,构造函数y=$\frac{a}{x}$+2x-4,
∵y=$\frac{a}{x}$+2x-4
∴当x=1时,函数有最小值a-2,
当x=2时,函数有最大值$\frac{a}{2}$,即a-2≤y≤$\frac{a}{2}$,
∵函数y=$\frac{a}{x}$与y=-2x+4在1≤x≤2上是“相邻函数”,
∴-1≤y1-y2≤1,即$\left\{\begin{array}{l}{\frac{a}{2}≤1}\\{a-2≥-1}\end{array}\right.$,
∴1≤a≤2;
∴a的最大值是2,a的最小值1.
点评 此题主要考查了反比例函数综合以及函数增减性和新定义,根据题意正确理解“相邻函数“的定义是解题关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案| A. | k=±2 | B. | k=2 | C. | k≥-1 | D. | k=-2 |
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | -$\frac{1}{2016}$ | D. | 2016 |
| A. | x6÷x2=x3 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | $\sqrt{18}$×$\sqrt{2}$=6 | D. | (a-2)2=a2-2a+4 |
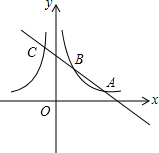 函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数
函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)的图象关于y轴对称,我们定义函数y=$\frac{k}{x}$和y=-$\frac{k}{x}$(k≠0)相互为“影像”函数 已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG.
已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: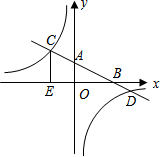 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.