题目内容
9.矩形两条对角线的夹角为60°,对角线长为10cm,则矩形的宽为5.分析 由题意可利用矩形的对角线相等,且互相平分,结合题意又知∠ADC=60°,则△ADC形成等边三角形而求得.
解答  解:由题意如图
解:由题意如图
由题意∠ADC=60°,
∵四边形ABEC是矩形,
∴对角线相等且平分:BC=AE且DB=DC=DE=AD,
∴△ADC是等边三角形,
∴AC=$\frac{1}{2}$AE=$\frac{1}{2}$×10=5cm.
故答案为:5.
点评 本题考查了矩形的性质,主要考查了矩形的对角线相等,且互相平分.由∠ADC=60°则△ADC形成等边三角形是本题的关键.

练习册系列答案
相关题目
19.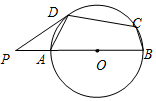 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
17.下列说法:①无理数是无限不循环小数;②有理数与数轴上的点一一对应;③$\frac{π}{2}$是分数;④2$\sqrt{3}$<3$\sqrt{2}$;⑤±3是$\sqrt{9}$的平方根,其中错误的有( )
| A. | ①②③ | B. | ②③④ | C. | ②③⑤ | D. | ③④⑤ |
4.方程3x+y=6的正整数解有( )
| A. | 1组 | B. | 2组 | C. | 4组 | D. | 无数组 |
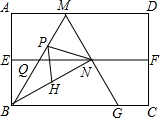 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.