题目内容
1.观察下列一组数:$\frac{1}{6}$,$\frac{4}{25}$,$\frac{8}{62}$,$\frac{13}{123}$…,它们是按一定规律描列的,那么这一组数的第n2个数是$\frac{\frac{1}{2}{n}^{4}+\frac{3}{2}{n}^{2}-1}{{n}^{6}+{3n}^{4}+{3n}^{2}-1}$.分析 首先根据已知发现分子的变化规律为1+3=4,4+4=8,8+5=13,13+6=19,…第n项的分子为1+3+4+5+…+(n+1)=$\frac{1}{2}$n2+$\frac{3}{2}$n-1;分母为6=23-2,25=33-2,62=43-2,123=53-2,…第n项的分母为(n+1)3-2=n3+3n2+3n-1,由此可得第n项;易得n2项.
解答 解:由已知得,
分子为1+3=4,4+4=8,8+5=13,13+6=19,
…
∴第n项的分子为1+3+4+5+…+(n+1)=1+$\frac{1}{2}$(3+n+1)(n-1)=$\frac{1}{2}$n2+$\frac{3}{2}$n-1,
分母为6=23-2,25=33-2,62=43-2,123=53-2,
…
∴第n项的分母为(n+1)3-2=n3+3n2+3n-1,
∴第n个数为$\frac{\frac{1}{2}{n}^{2}+\frac{3}{2}n-1}{{n}^{3}+{3n}^{2}+3n-1}$
∴n2个数为:$\frac{\frac{1}{2}{n}^{4}+\frac{3}{2}{n}^{2}-1}{{n}^{6}+{3n}^{4}+{3n}^{2}-1}$.
故答案为:$\frac{\frac{1}{2}{n}^{4}+\frac{3}{2}{n}^{2}-1}{{n}^{6}+{3n}^{4}+{3n}^{2}-1}$.
点评 本题主要考查了数字的变化规律,发现分子分母的变化规律,求出第n个数是解答此题的关键.

练习册系列答案
相关题目
11. 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )| A. | $\sqrt{17}$ cm | B. | 4cm | C. | $\sqrt{15}$ cm | D. | $\sqrt{3}$ cm |
6.下列长度的四根木棒,能与长度分别为2cm和5cm的木棒构成三角形的是( )
| A. | 3 | B. | 4 | C. | 7 | D. | 10 |
11.甲、乙两名运动员在某项射击比赛中10次射击的平均成绩都是7环,而甲、乙的成绩的方差分别为1.21和3.12,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
 如图是由一些小正方体组合而成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则这个几何体主视图是( )
如图是由一些小正方体组合而成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则这个几何体主视图是( )



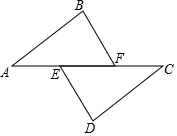 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.