题目内容
19.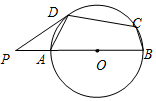 如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )
如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
分析 延长DO交⊙O于E,连接AC、AE.承办方求出∠ADO,根据切线的性质∠ODP=90°,根据∠PDA=90°-∠ADO即可解决问题.
解答 解:延长DO交⊙O于E,连接AC、AE.
∵AB是直径,
∴∠ACB=90°,∵∠DCB=115°,
∴∠DCE=∠E=25°,
∵DE是直径,
∴∠DAE=90°,
∴∠ADE=90°-25°=65°,
∵PD是⊙O的切线,
∴∠PDO=90°,
∴∠PDA=90°-∠ADO=25°.
故选A.
点评 本题考查切线的性质、直径的性质、圆内接四边形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若整数a使关于x的不等式组$\left\{\begin{array}{l}\frac{x+1}{2}≤\frac{2x+5}{6}\\ x-2>a\end{array}$至少有4个整数解,且使关于x的分式方程$\frac{12-ax}{x+2}$=2有整数解,那么所有满足条件的a的和是( )
| A. | -20 | B. | -17 | C. | -14 | D. | -23 |
7.下列各式中计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | 3x2=6x2 | C. | a2+a2=a4 | D. | (x2)3=x6 |
4.某校女子排球队队员的年龄分布如下表
则该校女子排球队队员的年龄中位数是13岁.
| 年龄(岁) | 13 | 14 | 15 |
| 人数(人) | 8 | 4 | 3 |
11. 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )| A. | $\sqrt{17}$ cm | B. | 4cm | C. | $\sqrt{15}$ cm | D. | $\sqrt{3}$ cm |
8.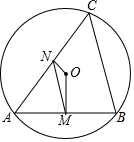 如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
 如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )
如图,△ABC内接于⊙O,OM⊥AB,ON⊥AC,垂足分别为M,N,连接MN,若AB=4,AC=6,∠A=60°.设MN=m,则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\frac{1}{2}$$\sqrt{3}$ | D. | $\frac{1}{2}\sqrt{2}$ |