题目内容
20．已知 25x2-144=0，求代数式2$\sqrt{5x+13}$的值．分析 依据平方根的定义求得x的值，然后代入计算即可．
解答 解：∵25x2-144=0，
∴x2=$\frac{144}{25}$．
∴x=±$\frac{12}{5}$．
当x=$\frac{12}{5}$时，2$\sqrt{5x+13}$=2$\sqrt{25}$=2×5=10；
当x=-$\frac{12}{5}$时，2$\sqrt{5x+13}$=2×1=2．
点评 本题主要考查的是算术平方根的性质，熟练掌握算术平方根的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
10．若整数a使关于x的不等式组$\left\{\begin{array}{l}\frac{x+1}{2}≤\frac{2x+5}{6}\\ x-2＞a\end{array}$至少有4个整数解，且使关于x的分式方程$\frac{12-ax}{x+2}$=2有整数解，那么所有满足条件的a的和是（ ）
| A． | -20 | B． | -17 | C． | -14 | D． | -23 |
11．
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为（ ）
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为（ ）| A． | $\sqrt{17}$ cm | B． | 4cm | C． | $\sqrt{15}$ cm | D． | $\sqrt{3}$ cm |
8．
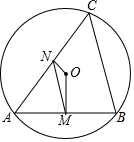如图，△ABC内接于⊙O，OM⊥AB，ON⊥AC，垂足分别为M，N，连接MN，若AB=4，AC=6，∠A=60°．设MN=m，则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是（ ）
如图，△ABC内接于⊙O，OM⊥AB，ON⊥AC，垂足分别为M，N，连接MN，若AB=4，AC=6，∠A=60°．设MN=m，则最简二次根式$\sqrt{{m}^{2}+1}$代入m值后的结果是（ ）| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | $\frac{1}{2}$$\sqrt{3}$ | D． | $\frac{1}{2}\sqrt{2}$ |
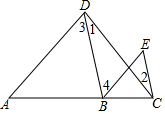按图填空，并注明理由
如图是由一些小正方体组合而成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，则这个几何体主视图是（ ）
