题目内容
19.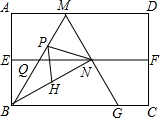 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.(1)连接AN,求证:△ABN是等边三角形;
(2)求AM、QN的长;
(3)P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是多少?
分析 (1)首先根据EF垂直平分AB,可得AN=BN;然后根据折叠的性质,可得AB=BN,据此判断出△ABN为等边三角形.
(2)首先根据∠ABN=60°,∠ABM=∠NBM,求出∠ABM=∠NBM=30°;然后在Rt△ABM中,根据AB=2,求出AM的大小即可;首先根据EF∥BC,QN是△MBG的中位线,可得QN=$\frac{1}{2}$BG;然后根据BG=BM=AB÷cos∠ABM=2÷$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$,求出QN的长度即可.
(3)根据∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,推得∠MBG=∠BMG=∠BGM=60°,即可推得△BMG是等边三角形;点N是MG的中点,判断出BN⊥MG,即可求出BN的大小;然后根据E点和H点关于BM称可得PH=PE,因此P与Q重合时,PN+PH=PN+PE=EN,据此求出PN+PH的最小值是多少即可.
解答  (1)证明:如图,连接AN,
(1)证明:如图,连接AN,
∵EF垂直平分AB,
∴AN=BN,
根据折叠的性质,可得
AB=BN,
∴AN=AB=BN.
∴△ABN为等边三角形.
(2)∵∠ABN=60°,∠ABM=∠NBM,
∴∠ABM=∠NBM=60°÷2=30°,
∴AM=AB•tan30°=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∵EF∥BC,QN是△MBG的中位线,
∴QN=$\frac{1}{2}$BG;
∵BG=BM=AB÷cos∠ABM=2÷$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$,
∴QN=$\frac{1}{2}$×$\frac{4\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$;
(3)∵∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,
∴∠BMG=∠BNM-∠MBN=90°-30°=60°,
∴∠MBG=∠ABG-∠ABM=90°-30°=60°,
∴∠BGM=180°-60°-60°=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,
∵点N是MG的中点,
∴BN⊥MG,
∴BN=BG•sin60°=$\frac{4\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=2,
根据条件易知E点和H点关于BM对称,∴PH=PE,
∴P与Q重合时,PN+PH的值最小,此时PN+PH=PN+PE=EN,
∵EN=$\sqrt{B{N}^{2}-B{E}^{2}}$=$\sqrt{{2}^{2}-(\frac{2}{2})^{2}}$=$\sqrt{3}$,
∴PN+PH=$\sqrt{3}$,
∴PN+PH的最小值是$\sqrt{3}$.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了等边三角形的判定和性质的应用,以及矩形的性质和应用,要熟练掌握.
(3)此题还考查了折叠的性质和应用,以及余弦定理的应用,要熟练掌握.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
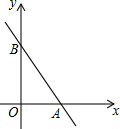 如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.
如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.