题目内容
4．方程3x+y=6的正整数解有（ ）| A． | 1组 | B． | 2组 | C． | 4组 | D． | 无数组 |
分析 首先用x表示出y，由于y大于0，可求得x的取值范围，再结合x、y都是正整数即可得解．
解答 解：3x+y=6，y=6-3x；
∵y＞0，故6-3x＞0，
∴0＜x＜2，因此x=1，
代入方程中，可求得y=3，
即方程的正整数解为$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$，
故选：A．
点评 此题主要考查的是二元一次方程以及不定方程的解法，能根据已知条件判断出x、y的取值范围是解决问题的关键．
练习册系列答案
新编小学单元自测题系列答案
相关题目
如图是由一些小正方体组合而成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，则这个几何体主视图是（ ）
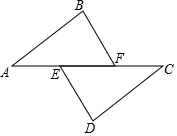在下面过程中的横线上填空，并在括号内注明理由．