题目内容
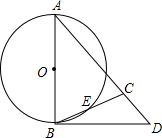 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=| 1 |
| 2 |
考点:弦切角定理
专题:
分析:连接AE,利用等腰三角形的性质易证∠BAE=∠CAE=
∠CAB,由弦切角定理可得∠CBD=∠BAE,所以∠CBD=
∠CAB.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=
∠CAB,
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD=
∠CAB.

∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=
| 1 |
| 2 |
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD=
| 1 |
| 2 |
点评:本题考查了弦切角定理的运用、圆周角定理以及等腰三角形的性质,解题的关键是正确的添加辅助线,利用等腰三角形的性质解题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
以下列各组数为三角形的边长,能构成直角三角形的是( )
| A、8,1,17 |
| B、3,5,7 |
| C、6,8,10 |
| D、5,10,12 |
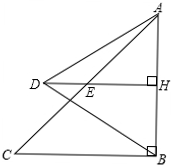 已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2.
已知,如图:△ABC是等腰直角三角形,∠ABC=90°,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于E,已知AD=BD=2.