题目内容
已知（x3+mx+n）（x2-5x+3）的乘积中不含x3和x2项，求m、n的值．
考点：多项式乘多项式
专题：计算题
分析：原式利用多项式乘以多项式法则计算，根据结果不含x3和x2项，求出m与n的值即可．
解答：解：（x3+mx+n）（x2-5x+3）=x5-5x4+（3+m）x3-（5m-n）x2+（3m-5n）x+3n，
由结果不含x3和x2项，得到3+m=0，5m-n=0，
解得：m=-3，n=-15．
由结果不含x3和x2项，得到3+m=0，5m-n=0，
解得：m=-3，n=-15．
点评：此题考查了多项式乘以多项式，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
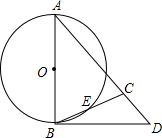如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于E，过B作⊙O的切线，交AC的延长线于D．求证：∠CBD=点A在x轴的负半轴上，则点A的坐标可能是下列的（ ）
| A、（0，3） |
| B、（0，-3） |
| C、（3，0） |
| D、（-3，0） |
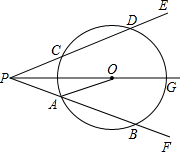如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心、10为半径作⊙O，分别与∠EPF的两边相交于A，B和C，D，连接OA，此时有OA∥PE，若弦AB=12，求OP的长．
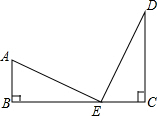如图，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：