题目内容
已知x2+y2+z2≤2x+4y-6z-14，求x2+y2+z2的值．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：把14分成1+4+9，与剩余的项构成3个完全平方式，从而出现三个非负数的和等于0的情况，则每一个非负数等于0，解即可．
解答：解：∵x2+y2+z2≤2x+4y-6z-14，
∴x2+y2+z2-2x-4y+6z+14≤0，
∴x2-2x+1+y2-4y+4+z2+6z+9≤0，
∴（x-1）2+（y-2）2+（z+3）2≤0，
∴x-1=0，y-2=0，z+3=0，
∴x=1，y=2，z=-3，
故x2+y2+z2=1+4+9=14．
∴x2+y2+z2-2x-4y+6z+14≤0，
∴x2-2x+1+y2-4y+4+z2+6z+9≤0，
∴（x-1）2+（y-2）2+（z+3）2≤0，
∴x-1=0，y-2=0，z+3=0，
∴x=1，y=2，z=-3，
故x2+y2+z2=1+4+9=14．
点评：本题考查了完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．
练习册系列答案
口算能手系列答案
相关题目
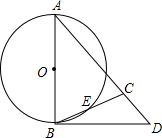如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于E，过B作⊙O的切线，交AC的延长线于D．求证：∠CBD=
”表示3abc，“方框
”表示（xm+yn），则
=
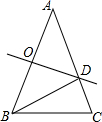如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，则下列结论：①BD平分∠ABC；②AD=BD=BC；③△BCD的周长等于AB+BC；④∠C=2∠A；⑤S△BCD=S△ABD，正确的个数（ ）