题目内容
若等腰△ABC内接于⊙O,若⊙O半径是5cm,底边CB长8cm,则这个等腰三角形的腰AB的长为 .
考点:垂径定理,等腰三角形的性质,勾股定理
专题:计算题
分析:连结OB,作OD⊥BC于D,根据垂径定理得BD=CD=
BC=4,再利用等腰三角形的性质得到点点A、O、D共线,解着在Rt△BOD中利用勾股定理计算出OD=3,然后分类讨论:当△ABC为锐角三角形时,如图1,AD=AO+OD=8;当△ABC为钝角三角形时,如图2,AD=AO-OD=2,再利用勾股定理分别计算AB即可.
| 1 |
| 2 |
解答:解: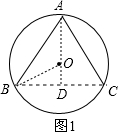 连结OB,作OD⊥BC于D,则BD=CD=
连结OB,作OD⊥BC于D,则BD=CD=
BC=4,
∴OD垂直平分BC,
而AB=AC,
∴点A在直线OD上,即点A、O、D共线,
在Rt△BOD中,∵OB=5,BD=4,
∴OD=
=3,
当△ABC为锐角三角形时,如图1,AD=AO+OD=5+3=8
在Rt△ABD中,AB=
=4
,
当△ABC为钝角三角形时,如图2,AD=AO-OD=5-3=2,
在Rt△ABD中,AB=
=2
,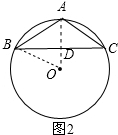
∴AB的长为2
cm或4
cm.
故答案为2
cm或4
cm.
 连结OB,作OD⊥BC于D,则BD=CD=
连结OB,作OD⊥BC于D,则BD=CD=| 1 |
| 2 |
∴OD垂直平分BC,
而AB=AC,
∴点A在直线OD上,即点A、O、D共线,
在Rt△BOD中,∵OB=5,BD=4,
∴OD=
| OB2-BD2 |
当△ABC为锐角三角形时,如图1,AD=AO+OD=5+3=8
在Rt△ABD中,AB=
| BD2+AD2 |
| 5 |
当△ABC为钝角三角形时,如图2,AD=AO-OD=5-3=2,
在Rt△ABD中,AB=
| BD2+AD2 |
| 5 |

∴AB的长为2
| 5 |
| 5 |
故答案为2
| 5 |
| 5 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的性质和勾股定理.利用垂径定理构建直角三角形是常用的方法,注意分类讨论.

练习册系列答案
相关题目
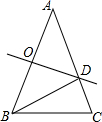 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,则下列结论:①BD平分∠ABC;②AD=BD=BC;③△BCD的周长等于AB+BC;④∠C=2∠A;⑤S△BCD=S△ABD,正确的个数( )| A、2个 | B、3个 | C、4个 | D、5个 |
如果等腰三角形的一腰上的高与另一腰的夹角为30°,则该等腰三角形顶角的度数是( )
| A、60° | B、120° |
| C、60°或120° | D、90° |
 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O(A不与O重合),连接AO,如果AB=6,AO=4
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O(A不与O重合),连接AO,如果AB=6,AO=4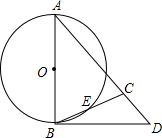 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=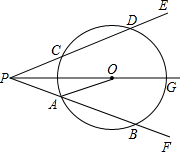 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心、10为半径作⊙O,分别与∠EPF的两边相交于A,B和C,D,连接OA,此时有OA∥PE,若弦AB=12,求OP的长.