题目内容
20.勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为(7$\sqrt{3}$+6,0).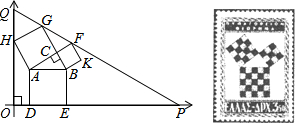
分析 在直角△ABC中,根据三角函数即可求得AC,进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长,在直角△QRP中运用三角函数即可得到RP、QP的长,解答即可.
解答 解:延长BA交QR于点M,连接AR,AP,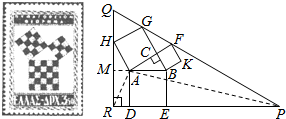 在△ABC与△GFC中,
在△ABC与△GFC中,
$\left\{\begin{array}{l}{AC=GC}\\{∠ACB=∠GCF}\\{BC=FC}\end{array}\right.$,
∴△ABC≌△GFC(SAS),
∴∠CGF=∠BAC=30°,
∴∠HGQ=60°,
∵∠HAC=∠BAD=90°,
∴∠BAC+∠DAH=180°,
又∵AD∥QR,
∴∠RHA+∠DAH=180°,
∴∠RHA=∠BAC=30°,
∴∠QHG=60°,
∴∠Q=∠QHG=∠QGH=60°,
∴△QHG是等边三角形.
AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}=2\sqrt{3}$,
则QH=HA=HG=AC=2$\sqrt{3}$,
在直角△HMA中,HM=AH•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.AM=HA•cos60°=$\sqrt{3}$,
在直角△AMR中,MR=AD=AB=4,
∴QR=2$\sqrt{3}$+3+4=7+2$\sqrt{3}$,
∴QP=2QR=14+4$\sqrt{3}$,
PR=QR•$\sqrt{3}$=7$\sqrt{3}$+6,
∴点P的坐标为(7$\sqrt{3}$+6,0).
故答案为:(7$\sqrt{3}$+6,0).
点评 此题考查勾股定理问题,正确运用三角函数以及勾股定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
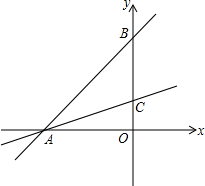 如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.
如图,直线y=x+1与x轴、y轴分别相交于点A、B,过点A的直线y=$\frac{1}{3}$x+b与y轴相交于点C.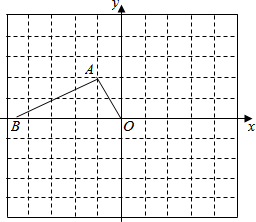 如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).
如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).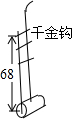 中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.
中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.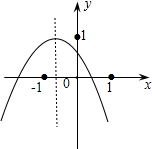 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )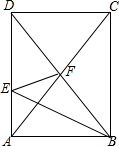 如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6.
如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6. 如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.
如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.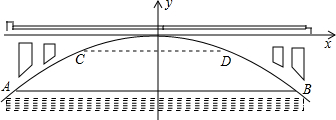
 已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH.
已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH.